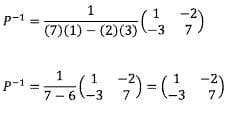Matriks – Operasi Matriks, Rumus, Contoh Soal Matriks dan Jawabannya Lengkap – Dalam matematika, matriks adalah susunan bilangan, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun persegi.
Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi.
Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan representasi matriks, perhitungan dapat dilakukan dengan lebih terstruktur. Dimensi matriks dapat berupa 2 x 3 (dua baris dan tiga kolom), 3 x 2 (tiga baris dan dua kolom) , 3 x 3 (tiga baris dan tiga kolom) dan lain-lain.
Pada umumnya, matriks ditulis dalam tanda kurung siku atau kurung kurawal “[]”.
Operasi Dasar Matriks
Penjumlahan dan Pengurangan Matriks
Penjumlahan dan pengurangan matriks hanya bisa dilakukan jika kedua matriks memiliki ukuran atau tipe yang sama. Elemen-elemen yang dijumlahkan atau dikurangi adalah elemen yang posisi atau letaknya sama.
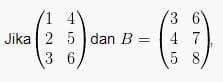
Penjumlahan Matriks
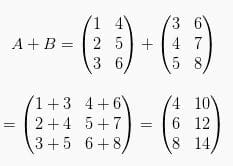
Pengurangan Matriks
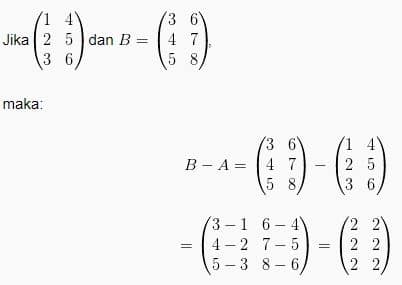
Sifat penjumlahan dan pengurangan matriks, diantaranya yaitu:
A + B = B + A
(A + B) + C = A + (B + C)
A – B ≠ B – A
Perkalian Matriks
Matriks dapat dikalikan dengan bilangan bulat maupun dengan matriks lain. Setiap perkalian matriks, memiliki syarat masing-masing, diantaranya yaitu:
a. Perkalian Matriks Dengan Bilangan Bulat atau Perkalian Skalar Matriks
Matriks bisa dikalikan dengan bilangan bulat, maka hasil perkalian tersebut berupa matriks dengan elemen-elemennya yang merupakan hasil kali antara bilangan dan elemen-elemen matriks tersebut. Jika matriks A dikali dengan bilangan r, maka r.A =(r.aij). Contohnya:
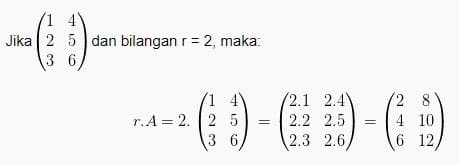
Perkalian matriks dengan bilangan bulat dikombinasikan dengan penjumlahan atau pengurangan matriks bisa dilakukan pada matriks dengan ordo sama. Berikut sifat-sifat perkaliannya:
r(A + B) = rA + rB
r(A – B) = rA – rB
b. Perkalian Dua Matriks
Perkalian antara dua matriks misalnya matriks A dan B, bisa dilakukan jika jumlah kolom A sama dengan jumlah baris B. Perkalian tersebut menghasilkan matriks dengan jumlah baris sama dengan matriks A dan jumlah saman dengan matriks B, sehingga:
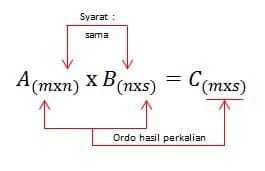
Elemen-elemen matriks C(mxs) merupakan penjumlahan dari hasil kali elemen-elemen baris ke-i matriks A dengan kolom ke-j matiks B. Berikut skemanya:
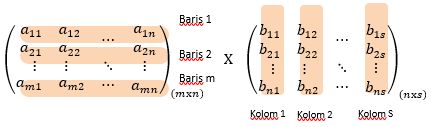
Misalnya matriks A berordo (3 x 4) dan matriks B berordo (4 x 2), maka matriks C berordo (3 x 2). Elemen C pada baris ke-2 dan kolom ke-2 atau a22 diperoleh dari jumlah hasil perkalian elemen-elemen baris ke-2 matriks A dan kolom ke-2 matriks B. Contohnya:

Perlu diingat sifat perkalian dua matriks bahwa:
A x B ≠ B x A
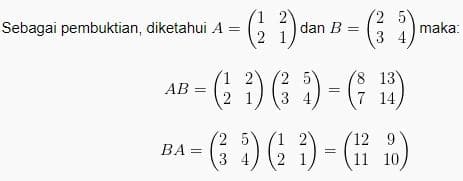
Terbukti bahwa A x B ≠ B x A. Ada sifat-sifat lain perkalian matriks dengan bilangan atau dengan matriks lain, sebagai berikut:
k(AB) = (kA)B
ABC = (AB)C = A(BC)
A(B + C) = AB + AC
(A + B)C = AC + BC
Determinan Matriks
Determinan dari matriks A diberi notasi tanda kurung, sehingga penulisannya |A|. Determinan hanya bisa dilakukan pada matriks persegi.
Determinan matriks ordo 2×2
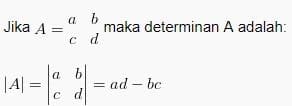
Determinan matriks ordo 3×3 (aturan Sarrus)

Berikut sifat-sifat determinan matriks:
1. Determinan A = Determinan AT
2. Tanda determinan berubah jika 2 baris/2 kolom yang berdekatan dalam matriks ditukar.
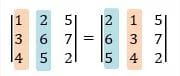
3. Apabila suatu baris atau kolom determinan matriks memiliki faktor p, maka p bisa dikeluarkan menjadi pengali.
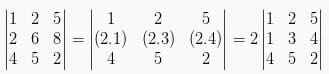
4. Apabila dua baris atau dua kolom merupakan saling berkelipatan, maka nilai determinannya adalah 0.
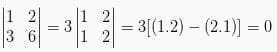
5. Nilai determinan dari matriks segitiga atas atau bawah adalah hasil kali dari elemen-elemen diagonal saja.
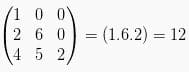
Invers Matriks
Suatu matriks A memiliki invers (kebalikan) jika ada matriks B yang dapat membentuk persamaan AB = BA = I, dengan I adalah matriks identitas. Invers dari suatu matriks berordo (2 x 2) seperti 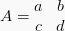 bisa dirumuskan sebagai:
bisa dirumuskan sebagai:
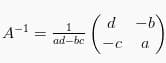
Berikut sifat-sifat invers matriks:
AA-1 = A-1A = I
(A-1)-1 = A
(AB)-1 = B-1A-1
Jika AX = B, maka X = A-1B
Jika XA=B, maka X = BA-1
Contoh Soal Matriks dan Pembahasan Matriks
1. Dua buah matriks A dan B masing-masing berturut-turut:
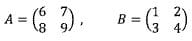
Maka, tentukan A-B
Pembahasan:
A-B =
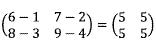
2. Perhatikan matriks P dan matriks Q, berikut ini.
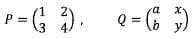
Tentukan matriks PQ
Pembahasan:
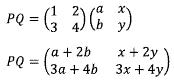
3. Dari dua buah matriks di bawah ini:
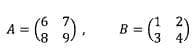
Tentukan 2A + B
Pembahasan:
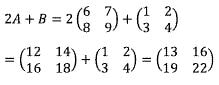
4. Tentukan determinan dari matriks A berikut ini
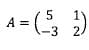
Pembahasan:
det A = |A| = ad − bc = (5)(2) − (1)(−3) = 10 + 3 = 13
5. Tentukan nilai a + b + x + y dari matriks berikut ini:
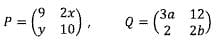
Diketahui bahwa P = Q
Pembahasan:
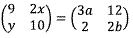
3a = 9 → a = 3
2b = 10 → b = 5
2x = 12 → x = 6
y = 6
y = 2
Sehingga:
a + b + x + y = 3 + 5 + 6 + 2 = 16
6. Tentukan tranpose dari matriks A berikut ini:
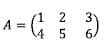
Jawab:
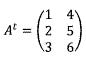
7. Tentukan invers dari matriks berikut ini:
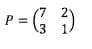
Pembahasan:
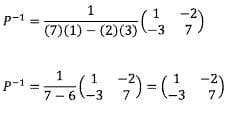
Demikian penjelasan yang bisa kami sampaikan tentang Matriks – Operasi Matriks, Rumus, Contoh Soal Matriks dan Jawabannya Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Artikel Paling Populer :
- Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan… Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya Lengkap – Dalam matematika membahas tentang bangun ruang. Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk…
- Proporsi Proporsi Perbandingan/rasio dan proporsi merupakan dasar utama untuk memahami berbagai konsep dalam matematika maupun sains. Proporsi mengatakan bahwa dua perbandingan (atau dua pecahan) adalah sama. Dengan kalimat lain dua buah perbandingan dikatakan…
- Pengertian, Cara Menentukan, Contoh Soal Rumus… Pengertian, Cara Menentukan, Contoh Soal Rumus Empiris dan Rumus Molekul Senyawa Lengkap – Rumus kimia merupakan salah satu ciri khas dari senyawa kimia. Rumus kimia terbagi menjadi 2 (dua) yaitu rumus…
- Himpunan Penyelesaian Persamaan Linear Satu Variabel Sebelumnya sudah dibahas bahwa kalimat terbuka yang dihubungkan oleh tanda sama dengan (=) disebut persamaan, sedangkan persamaan dengan satu variabel berpangkat satu atau berderajat satu disebut persamaan linear satu variabel. Bagaimana cara menentukan…
- Pembagian Apa itu Pembagian ? Pembagian adalah proses membagi kumpulan item menjadi bagian yang sama dan merupakan salah satu operasi aritmatika dasar dalam matematika. Kami mungkin menghadapi situasi yang berbeda setiap…
- Dinamika Gerak Rotasi : Pengertian, Rumus Dan… Dinamika Gerak Rotasi : Pengertian, Rumus Dan Pembahasan Contoh Soal – Aksi akrobat selalu menghadirkan decak kagum setiap orang yang menyaksikan. Atraksi yang sering dilakukan misalnya melipat tubuh dan menaiki roda yang…
- Pengertian Komunikasi Bisnis, Tujuan, Fungsi, Unsur… Pengertian Komunikasi Bisnis, Tujuan, Fungsi, Unsur dan Bentuk Komunikasi Bisnis Menurut Para Ahli Terlengkap – Secara umum, Komunikasi bisnis adalah pertukaran gagasan dan informasi yang memiliki tujuan tertentu yang disajikan secara…
- Penyelesaian PLSV dengan Persamaan-Persamaan yang Ekuivalen Sebelumnya kami sudah dibahas tentang cara penyelesain persamaan linear satu variabel dengan cara substitusi (penggantian). Cara itu kelihatan agak ribet karena harus mencoba satu persatu suatu bilangan yang jumlahnya tidak terhingga.…
- Bentuk dan Unsur - Unsur Aljabar Tahukah Anda apa pengertian aljabar (algebra)? Menurut Wikipedia, aljabar (algebra) berasal dari Bahasa Arab "al-jabr" yang artinya "hubungan" atau "penyelesaian". Jadi, aljabar merupakan cabang ilmu matematika yang mempelajari hubungan dan penyelesaian…
- Bilangan Pangkat Pecahan : Pengertian, Rumus, Sifat… Bilangan Berpangkat Pecahan : Pengertian, Rumus, Sifat Operasi Hitung dan Contoh Soal Bilangan Pangkat Pecahan Lengkap – Bilangan berpangkat adalah bentuk perkalian bilangan-bilangan yang sama atau perkalian berulang, pangkat pada bilangan…
- Pengertian Sitoplasma, Fungsi, Struktur dan… Pengertian Sitoplasma, Fungsi, Struktur dan Bagian-Bagian Sitoplasma Lengkap – Sitoplasma adalah bagian sel yang terbungkus membran sel. Sitoplasma ini merupakan cairan pada sel yang terbungkus membran sel. Setiap sel memiliki…
- Operasi Penjumlahan dan Pengurangan Pecahan Operasi Penjumlahan dan Pengurangan Pecahan dapat dilakukan jika penyebut kedua atau lebih dari pecahan tersebut memiliki nilai yang sama. Penjumlahan dan Pengurangan Pecahan Yang Penyebutnya Sama Misalkan “Budi dan Iwan masing-masing…
- Gerak Melingkar Beraturan (GMB) Ada yang sudah mengenal atau pernah mendengar mengenai istilah Gerak Melingkar Beraturan (GMB)? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Gerak Melingkar Beraturan (GMB) Gerak Melingkar Beraturan (GMB) merupakan salah…
- Penjumlahan dan Pengurangan Pada Bentuk Aljabar Operasi hitung pada bentuk aljabar sama seperti operasi hitung pada bilangan bulat yang meliputi: penjumlahan, pengurangan, perkalian, pembagian dan perpangkatan. Nah pada postingan ini kami hanya membahas tentang penjumlahan dan…
- Rumus Barisan Dan Deret Aritmatika Beserta Contoh… Rumus Barisan Dan Deret Aritmatika Beserta Contoh Soal Dan Penyelesaian Lengkap – Aritmatika atau Aritmetika berasal dari bahasa yunani αριθμός yang berarti angka yang dulu biasa disebut dengan Ilmu Hitung yaitu cabang tertua atau pendahulu…
- Penerapan Pertidaksamaan Linear Satu Variabel Untuk mengerjakan soal-soal pertidaksamaan linear satu variabel yang berkaitan dengan permasalahan dalam kehidupan sehari-hari caranya hampir sama seperti mengerjakan soal-soal persamaan linear satu variabel (Silahkan baca penerapan persamaaan linear satu variabel).…
- Pengertian, Ciri, Fungsi, Penyusun, Macam-Macam dan… Pengertian, Ciri, Fungsi, Penyusun, Macam-Macam dan Letak Jaringan Ikat Pada Manusia Terlengkap – Jaringan ikat adalah jaringan yang berfungsi mengikat, menyokong dan menambat bagian jaringan maupun organ lainnya. Penyusun jaringan ikat…
- Tulang Rawan Ada yang sudah mengenal atau pernah mendengar mengenai istilah Tulang Rawan? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Tulang Rawan Tulang rawan merupakan salah satu jaringan ikat di mana tulang…
- Sitoplasma Adalah Ada yang sudah mengenal atau pernah mendengar mengenai istilah Sitoplasma? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Sitoplasma Sitoplasma merupakan salah satu cairan pada sel yang terbungkus membran sel. Tiap-tiap…
- Pengertian Pola Bilangan : Macam Jenis dan Contoh… Pengertian Pola Bilangan : Macam Jenis dan Contoh Pola Bilangan Sebelum mempelajari barisan aritmatika dan barisan geometri, ada sub bab materi barisan bilangan atau bab yang perlu dipahami terlebih dahulu yaitu pola…
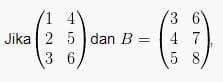
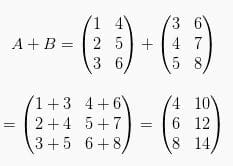
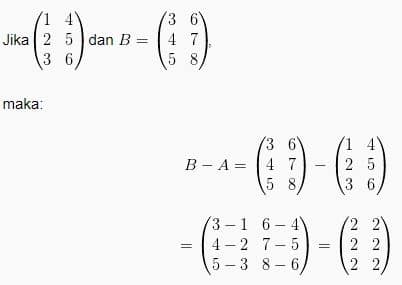
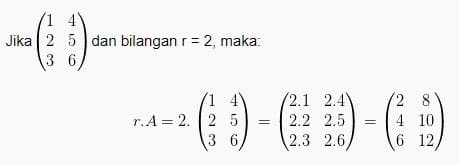



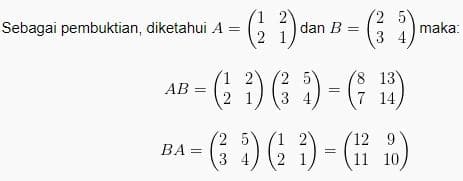
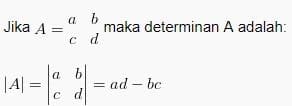

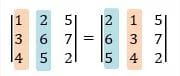
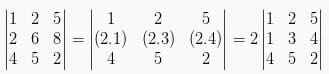
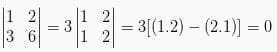
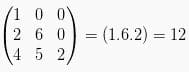
![]() bisa dirumuskan sebagai:
bisa dirumuskan sebagai: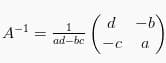
![]()
![]()
![]()
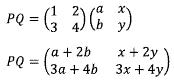
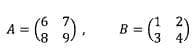
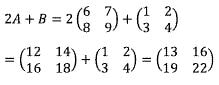
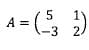
![]()
![]()
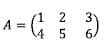
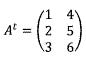
![]()