Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya Lengkap – Dalam matematika membahas tentang bangun ruang. Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya. Salah satu jenis bangun ruang yaitu kerucut, apa itu kerucut? Agar lebih memahaminya, kita akan membahas materi kerucut, rumus dan contoh soal bangun ruang kerucut secara lengkap.
Pengertian Kerucut
Pengertian kerucut adalah salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran.
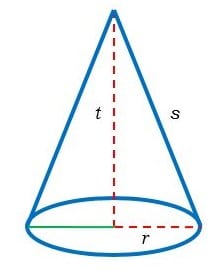
Sisi tegak pada kerucut ini berupa bidang miring yang disebut selimut kerucut. Sisi lainnya disebut alas kerucut. Maka dapat disimpulkan, bahwa kerucut hanya memiliki 2 sisi, dan satu rusuk. Lebih jelasnya, berikut gambar kerucut:
Ciri-Ciri Bangun Ruang Kerucut
Ciri ciri kerucut diantaranya yaitu:
- Kerucut merupakan bangun ruang berbentuk limas yang alasnya berbentuk lingkaran.
- Kerucut memiliki 2 sisi.
- Kerucut memiliki 1 rusuk.
- Kerucut memiliki 1 titik puncak.
- Kerucut memiliki jaring-jaring kerucut yaitu lingkaran dan segi tiga.
Sifat- Sifat Bangun Ruang Kerucut
Sifat-sifat kerucut, diantaranya:
- Kerucut memiliki 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
- Kerucut memiliki 1 rusuk lengkung
- Kerucut tidak memiliki rumus titik sudut.
- Kerucut memiliki 1 buah titik puncak.
Unsur-Unsur Kerucut
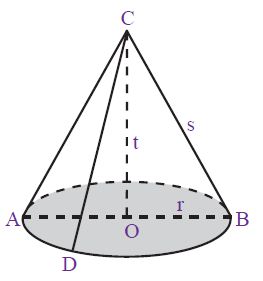
Perhatikan, gambar diatas diperoleh unsur unsur kerucut seperti:
Bidang alas, yaitu sisi yang berbentuk lingkaran (daerah yang diarsir).
Diameter bidang alas (d), yaitu ruas garis AB.
Jari-jari bidang alas (r), yaitu garis OA dan ruas garis OB.
Tinggi kerucut (t), yaitu jarak dari titik puncak kerucut ke pusat bidang alas (ruas garis CO).
Selimut kerucut, yaitu sisi kerucut yang tidak diarsir.
Garis pelukis (s), yaitu garis-garis pada selimut kerucut yang ditarik dari titik puncak C ke titik pada lingkaran.
Hubungan antara r, s, dan t pada kerucut tersebut di atas dapat dinyatakan dengan persamaan-persamaan berikut, yang bersumber dari teorema pythagoras, yaitu:
s² = r² + t²
r² = s² – t²
t² = s² – r²
Rumus Kerucut
Rumus Volume Kerucut
V = 1/3πr².t
Rumus Luas Permukaan Kerucut
L = Luas Lingkaran + Luas Selimut
L = πr²+ trs atau
L = πr. (r+s)
Rumus Luas Alas Kerucut
L = πr²
Rumus Luas Selimut Kerucut
L = πrs
Keterangan:
r = jari- jari (cm)
T = tinggi(cm)
π = 22/7 atau 3,14
Contoh Soal Bangun Ruang Kerucut dan Pembahasannya
1. Sebuah lingkaran memiliki luas 40 cm². Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.
Jawab:
Diketahui:
t = 9 cm
Luas : L = π x r² = 40 cm²
V = 1/3 x π x r² x t
= 1/3 x 40 x 9 (ingat : π x r² = 40 cm²)
= 120 cm³.
Jadi, volume kerucut adalah 120 cm³.
2. Diketahui sebuah kerucut dengan tinggi 8 cm. Apabila jari-jarinya yaitu 16 cm, berapakah volume bangun tersebut?
V = 1/3πr². t
V = 1/3 x 22/7 x 16 x 16 x 8
V = 2.124 cm³
3. Sebuah kerucut memiliki tinggi 16 cm. Apabila jari-jari kerucut tersebut 10 cm, berapakah volume dari bangun tersebut? (π = 3,14)
V = 1/3 x 3,14 x 10 x 10 x 16 = 1657 cm³
4. Diketahui sebuah kerucut dengan volume ialah 8.300 cm³. Tentukanlah diameter kerucut tersebut apabila tingginya 20 cm! (π = 22/7)
V = 1/3πr².t
8.300 = 1/3 x 22/7 x r² x 20
8.300 = 147/7 x r²
r² = 8.316 x 7/147
r² = 396
r = √396
r = 19.9 cm
Maka:
d = 2r
d = 2 x 19.9
d = 39.8 cm
5. Sebuah kerucut memiliki panjang jari-jari alas yaitu 6 cm dan tinggi 8 cm. Berapakah luas kerucut tersebut ( π = 3,14).
Jawab :
r = 6cm
t = 8 cm
s² = r² + t²
s² = 6²+ 8² = 36 + 64 = 100
s =√100 = 10
Luas sisi kerucut = πr(r + s)
= 3,14 x 6 x (6 + 10) = 3,14 x 6 x l6 = 301,44
Maka, luas sisi kerucut yaitu 301,44 cm²
6. Sebuah topi ulang tahun memiliki bentuk kerucut yang mempunyai ukuran jari-jari 28 cm dan tingginya 10 cm, berapakah Volume topi tersebut ?
Jawab :
r = 28 cm
t = 10 cm
V = x luas alas x tinggi
V = x πr2 x t
V = πr2 t
V = x x 282 x 10 cm
V = 8.213,3 cm³
Demikian materi pembahasan tentang bangun ruang kerucut dan contoh soalnya lengkap semoga bermanfaat.
Artikel Paling Populer :
- Materi, Rumus, dan Contoh Kalimat Past Continuous Tense Materi, Rumus, dan Contoh Kalimat Past Continuous Tense - Di kesempatan kali ini kami akan membahas tentang Past Continuous Tense. Sesuai dengan judulnya, Past Continuous Tense adalah sebuah tense yang menunjukkan…
- Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan… Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan Tata Nama Senyawa Kimia Beserta Contohnya Lengkap – Senyawa kimia adalah zat kimia murni yang terdiri dari dua atau beberapa unsur yang bisa…
- Past Future Continuous Tense: Pengertian, Rumus, dan… Past Future Continuous Tense – Pola tense ini menggabungkan tiga waktu yaitu bentuk past (lalu), future, dan continuous (sedang berlangsung). Seperti yang kita tahu bahwa bentuk past selalu menggunakan verb 2, bentuk future menggunakan will, dan bentuk continuous menggunakan present participle. Kombinasi…
- Pengertian dan Contoh Besaran Pokok dan Turunan Berdasarkan asal satuannya besaran aecara fisika dibagi menjadi dua yaitu besaran pokok dan besaran turunan. Apa itu besaran pokok dan turunan? Besaran pokok adalah besaran yang satuannya didefinisikan tersendiri, telah ditetapkan…
- Pengertian, Sifat, Rumus, Spektrum, Manfaat dan… Pengertian, Sifat, Rumus, Spektrum, Manfaat dan Contoh Soal Gelombang Elektromagnetik Lengkap – Gelombang elektromagnetik adalah gelombang yang memancar tanpa media rambat yang membawa muatan energi listrik dan magnet (elektromagnetik). Gelombang elektromagnetik…
- Garis dan Sudut serta sifat-sifatnya Garis dan Sudut adalah bentuk dasar dalam geometri. Garis adalah gambar yang terdiri dari titik-titik tak terhingga yang membentang tanpa batas di kedua arah. Dengan kata lain, garis dibentuk oleh…
- Sifat-Sifat Segitiga Istimewa sekarang akan membahas sifat-sifat segitiga secara spesifik yaitu segitiga istimewa. Apa itu segitiga istimewa dan bagaimana sifat-sifatnya? Segitiga istimewa adalah segitiga yang mempunyai sifat-sifat khusus (istimewa). Dalam hal ini ada…
- Rumus Dan Pembahasan Contoh Soal Persamaan Lingkaran… Rumus Dan Pembahasan Contoh Soal Persamaan Lingkaran Matematika Lingkaran adalah tempat kedudukan atau himpunan titik titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu tersebut dinamakan pusat lingkaran dan…
- Pengertian Proyeksi Peta, Lengkap Jenis dan Macam-Macamnya Penjelasan Pengertian Proyeksi Peta, Lengkap Jenis dan Macam-Macam Proyeksi Peta Proyeksi peta merupakan upaya memindahkan garis-garis paralel dan meridian dari bidang lengkung (globe) ke bidang datar. Di dalam upaya itu…
- Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus… Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus dan Contoh Soal Balok Beserta Cara Penyelesaian – Balok adalah bangun ruang 3 dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling…
- Sifat-Sifat Segitiga Secara Umum Kita sudah mengetahui pengertian dan jenis-jenis segitiga. Sekarang kita aka membahas mengenai sifat-sifat segitiga pada umum. Secara umum segitiga akan memeneuhi konsep ketidaksamaan segitiga, hubungan sudut dalam segitiga, dan hubungan sudut…
- 54 Kumpulan Gambar Jaring-Jaring Balok Lengkap… 54 Kumpulan Gambar Jaring-Jaring Balok Lengkap Dengan Contoh Soal dan Jawaban – Balok adalah bangun ruang 3 dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling tidak ada sepasang diantaranya…
- Pengertian Tenaga Endogen, Jenis dan Contoh Tenaga… Pengertian Tenaga Endogen, Jenis dan Contoh Tenaga Endogen Lengkap – Tenaga endogen adalah tenaga yang berasal dari dalam bumi yang menyebabkan perubahan pada kulit bumi. Tenaga endogen ini sifatnya membentuk…
- Pengertian Pola Bilangan : Macam Jenis dan Contoh… Pengertian Pola Bilangan : Macam Jenis dan Contoh Pola Bilangan Sebelum mempelajari barisan aritmatika dan barisan geometri, ada sub bab materi barisan bilangan atau bab yang perlu dipahami terlebih dahulu yaitu pola…
- Cermin Cekung : Pengertian, Sinar Istimewa, Sifat… Cermin Cekung: Pengertian, Sinar Istimewa, Sifat Bayangan, Rumus dan Contoh Soal Cermin Cekung Terlengkap – Cermin cekung merupakan cermin yang berbentuk lengkung, dimana permukaan cermin cekung yang memantulkan cahaya melengkung…
- Pengertian Sitoplasma, Fungsi, Struktur dan… Pengertian Sitoplasma, Fungsi, Struktur dan Bagian-Bagian Sitoplasma Lengkap – Sitoplasma adalah bagian sel yang terbungkus membran sel. Sitoplasma ini merupakan cairan pada sel yang terbungkus membran sel. Setiap sel memiliki…
- Pengertian dan Jenis-Jenis Wilayah Secara Umum dan… Pengertian dan Jenis-Jenis Wilayah Secara Umum dan Menurut Para Ahli Lengkap – Wilayah adalah sebuah daerah yang dikuasai atau menjadi teritorial dari sebuah kedaulatan. Secara umum, wilayah atau region adalah suatu…
- Pengertian, Sifat, Rumus, Spektrum, Manfaat dan… Pengertian, Sifat, Rumus, Spektrum, Manfaat dan Contoh Soal Gelombang Elektromagnetik Lengkap – Gelombang elektromagnetik adalah gelombang yang memancar tanpa media rambat yang membawa muatan energi listrik dan magnet (elektromagnetik). Gelombang elektromagnetik…
- Pengertian, Sifat, Jenis, Rumus dan Contoh Soal… Pengertian, Sifat, Jenis, Rumus dan Contoh Soal Trapesium Beserta Jawaban Lengkap – Trapesium adalah bangun datar dua dimensi tang dibentuk oleh 4 rusuk diantaranta saliung sejajar namun tidak sama panjang.…
- Lensa Cekung: Pengertian, Sifat, Jenis, Sinar… Lensa Cekung: Pengertian, Sifat, Jenis, Sinar Istimewa, Pembentukan Bayangan, Rumus dan Manfaat Lensa Cekung Terlengkap – Lensa cekung merupakan lensa yang bagian tengahnya lebih tipis dibandingkan dengan bagian tepinya yang…

