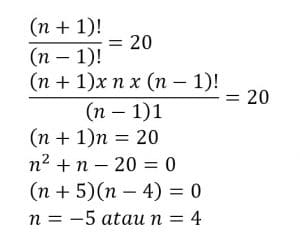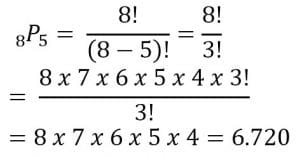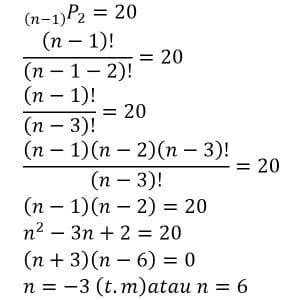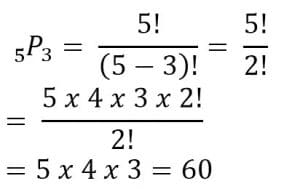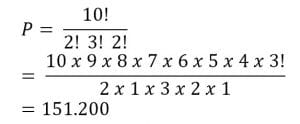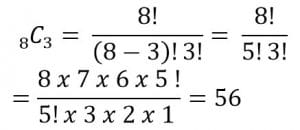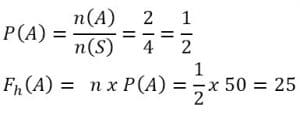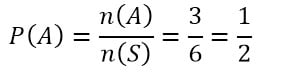15 Contoh Soal Dan Pembahasan Materi Peluang Kejadian Matematika

15 Contoh Soal Dan Pembahasan Materi Peluang Kejadian Matematika

Setelah kita bahas tentang peluang kejadian pada postingan sebelumnya, kali ini kita bahas tentang Contoh soal dan pembahasan materi peluang matematika. Untuk mengerjakan soal dibawah ini di sarankan kepada pembaca untuk memahami kembali materi peluang pada artikel : Materi Peluang Matematika , Pengertian Dan Rumus Soal terlengkap

Perhatikan dan simaklah soal soal tentang materi peluang keajdian dibawah ini:

Soal 1 -3 menggunakan rumus aturan perAnda

Nomor 1.

Dari 3 orang siswa akan dipilih untul menjadi ketua kelas, sekretaris dan benda hara dengan aturan bahwa seseorang tidak boleh merangkap jabatan pengurus kelas. Tentukan banyaknya cara pemilihan pengurus tersebut.

Penyelesaian:

Untuk posisi ketua kelas dapat dipilih dari 3 orang sehingga posisi ketua kelas dapat dipilih dengan 3 cara. Untuk posisi sekretaris karena ketua kelas sudah terisi oleh satu orang maka posisi sekretaris hanya dapat dipilih dari 2 orang yang belum terpilih menjadi pengurus kelas sehingga posisi sekretaris dapat dipilih dengan 2 cara, sedangkan untuk posisi bendahara karena posisi ketua kelas dan sekretaris sudah terisi maka posisi bendahara hanya ada satu pilihan sehingga posisi bendahara dapat dipilih dengan 1 cara.

Jadi, banyaknya cara pemilihan ada 3 x 2 x 1 = 6 cara.

Nomor 2.

Dari kota A ke kota B dapat dilalui 4 jalur, sedangkan dari kota B ke kota C dapat dilalui 2 jalur. Berapa jalur dapat dilalui dari kota A ke kota C melewati kota B?

Penyelesaian:

NAB = 4 jalur
NBC = 2 jalur
NAC = NAB x NAC
          = 4 x 2 = 8

Nomor 3.

Dari angka-angka 2,3,4,5,dan 6 akan dibuat bilangan ratusan dengan syarat tidak boleh ada angka yang diulang. Tentukan banyaknya bilangan yang terjadi.

Penyelesaian:

Ratusan Puluhan Satuan
5 4 3

Banyaknya bilangan = 5 x 4 x 3 = 60

Jadi, banyaknya bilangan ratusan yang terjadi ada 60 buah.

Soal n0 4 – 5 menggunakan rumus Factorial

Nomor 4.

Tentukan nilai dari 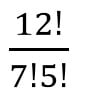1d

Penyelesaian:

2d

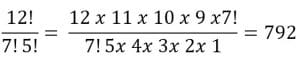
Nomor 5. 

Tentukan nilai n yang memenuhi 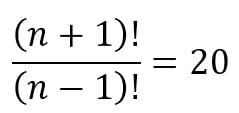3d

Penyelesaian: 

4d

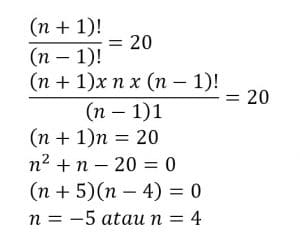
Jadi, nilai n yang memenuhi adalah = 4

Soal no 6 – 9 menggunakan rumus permutasi

Nomor 6.

Hitunglah nilai dari 8P5

Penyelesaian:

5d

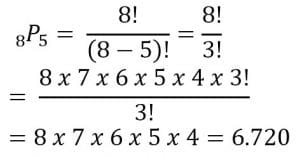
Nomor 7.

Tentukan nilai n apabila (n-1)P2=20

Penyelesaian:

6d

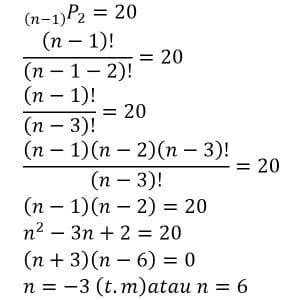
Jadi, nilai n adalah 6

Nomor 8. 

Dari 5 orang akan dipilih 3 orang untuk menjadi pengurus RT yang terdiri dari ketua, sekretaris dan bendahara. Tentukan banyaknya cara pemilihan yang mungkin.

penyelesaian:

7d

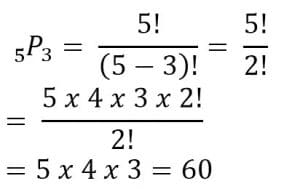
Jadi, banyaknya cara pemilihan adalah 60 cara.

Nomor 9.

Tentukan banyaknya susunan yang dapat dibuat dari kata “MATEMATIKA”

Penyelesaian:

n = 10 ; M = 2; A = 3 ; T = 2

8d

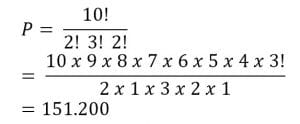
Jadi, banyaknya susunan kata yang dapat dibuat ada 151.200 buah.

Soal no 10 menggunakan rumus permutasi siklis

Nomor 10.

Pada suatu rapat dihadiri oleh 6 orang yang duudk mengelilingi sebuah meja bundar. Berapa banyak susunan duduk yang dapat terjadi?

Penyelesaian:

P = (n-1)!
= (6-1)!
= 5!
= 5 x 4 x 3 x 2 x 1
= 120

Jadi, banyaknya susunan duduk yang dapat terjadi ada 120 cara

Soal no 11 menggunakan rumus kombinasi

Nomor 11.

Tentukan nilai dari  C83

Penyelesaian:

9d

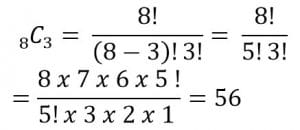
Soal no 12- 15 menggunakan rmus peluang suatu kejadian

Nomor 12.

Tentukan ruang sample dari pelemparan dua buah dadu

Penyelesaian:

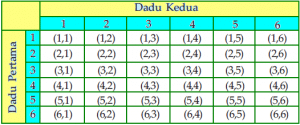
sampel dadu

Jadi ruang sampelnya adalah

{(1,1)(1,2)(1,3)(1,4)(1,5)(1,6)(2,1)(2,2)(2,3)(2,4)(2,5)(2,6)(3,1)(3,2)(3,3)(3,4)(3,5)(3,6)(4,1)(4,2)(4,3)(4,4)(4,5)(4,6)(5,1)(5,2)(5,3)(5,4)(5,5)(5,6)(6,1)(6,2)(6,3)(6,4)(6,5)(6,6)}

Nomor 13.

Dua buah uang logam dilempar undi sebanyak 50 kali. Berapakan frekuensi harapan muncul satu angka dan satu gambar?

Penyelesain:

n = 50 kali
S = {(A,A) (A,G) (G,A) (G,G)} → n (S) = 4
A = kejadian muncul satu angka dan satu gambar
= {(A,G) (G,A)} -> n (A) = 2

12d

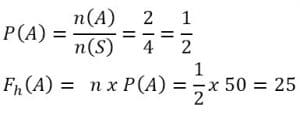
Nomor 14.

Sebuah dadu dilempar undi sekali. Berapa peluang muncul:

  • Mata dadu genap, dan
  • Mata dadu bukan genap

Penyelesaian:

S = { 1,2,3,4,5,6,) → n(S) = 6

  • Muncul mata dadu genap
    A = {2,4,6} → n (A) = 3
    13d
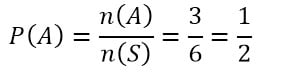
  • Muncul mata dadu bukan genap
    P(A) + p (Ac)=1
    ½ + P(Ac)=1
    P(Ac)= ½

Nomor 15.

Sebuah dadu dilempar undi sekali. Tentukan peluang muncul mata dadu genap atau prima.

Penyelesaian:

A = kejadian muntul mata dadu genap
= {2,4,6} → n(A) = 3
B = kejadian muncul mata dadu prima
= {2,3,5} → n(B) = 3

14d

 Demikian contoh soal dan pembahasan tentang materi peluang yang bisa kami sajikan untuk para pembaca. Semoga artikel ini bermanfaat  dan dapat membantu pembaca dalam mengerjakan tugas sekolah. Sampai bertemu pada artikel selanjutnya.. “TETAP SEMANGAT!”

Artikel Paling Populer :

  • Pengertian gaya Gesek dengan Rumus dan Contoh Soal… Pengertian Gaya Gesek Lengkap dengan Rumus dan Pembahasan Contoh Soal Gaya gesek merupakan gaya yang melawan gerak benda pada suatu permukaan yang terjadi akibat oleh dua permukaan benda yang bersentuhan.…
  • Materi dan Soal Bahasa Inggris Adverb Kelas 7 SMP Setelah mempelajari bahasa inggris selama ini kalian pasti bertanya-tanya mengenai struktur kalimat dan salah satunya adalah adverb. Apa itu adverb? Adverb adalah salah satu bagian dari part of speech yang…
  • Faktor Persekutuan Terbesar (FPB) Suatu Bilangan Bulat Sebelum membahas tentang faktor pesekutuan terbesar (FPB) dari dua atau lebih bilangan bulat, silahkan simak contoh soal berikut “Ibu Ani akan membuat parcel buah yang berisi tiga jenis buah yakni…
  • Pengertian Pangkat Tiga dan Akar Pangkat Tiga Pada postingan sebelumnya yang berjudul “Pengertian Perpangkatan Bilangan” sudah dijelaskan bahwa operasi perpangkatan merupakan perkalian berulang dengan unsur yang sama. Hal ini juga berlaku pada bilangan berpangkat tiga. Jadi, m3 =…
  • Materi Peluang Matematika , Pengertian Dan Rumus… Materi Peluang Matematika , Pengertian Dan Penjelasan Rumus Soal Peluang Terlengkap Tentunya kalian pernah melihat atau membaca data tentang bagaimana kondisi cuaca disuatu daerah? Apakah kondisinya cerah, hujan atau berawan…
  • Materi dan Soal Bahasa Inggris Preposition Kelas 7 SMP Hello para jagoan bahasa inggris. Di kesempatan ini kami akan memberikan penjelasan mengenai preposition. Kalian pasti sering menemui kata in, on, dan at dalam kalimat bahasa inggris. Nah itu merupakan…
  • Pengertian, Sifat, Rumus dan Contoh Soal Tekanan… Pengertian, Sifat, Rumus dan Contoh Soal Tekanan Hidrostatis Beserta Pembahasan Terlengkap – Tekanan hidrostatis adalah tekanan yang diakibatkan oleh gaya yang ada pada zat cair terhadap suatu luas bidang tekan…
  • Pembahasan Lengkap Aturan Cosinus Segitiga… Pembahasan Lengkap Aturan Cosinus Segitiga Trigonometri Dalam Ilmu Matematika – Teorema Pythagoras merupakan suatu rumus matematika yang sangat penting dalam geometri. Dengan menggunakan teorema phytagoras, kita bisa menghitung jarak antara dua…
  • Pengertian, Rumus & Contoh Soal Barisan Dan Deret… Pengertian, Rumus & Contoh Soal Barisan Dan Deret Geometri Beserta Penjelasan Lengkap – Terdapat dua jenis Barisan dan Deret di dalam matematika yaitu Barisan dan Deret Aritmatika & Barisan dan…
  • Perbandingan Segmen Garis Pada dasarnya materi perbandingan segmen garis hampir sama dengan perbandingan senilai atau seharga yang sudah diulas pada Materi matematika kelas VII Semester Ganjil pada postingan yang berjudul Cara Menghitung Perbandingan Seharga (senilai). Sebuah…
  • Menyelesaikan Masalah Dengan Menggunakan Konsep Himpunan Jika Anda amati masalah dalam kehidupan sehari-hari maka banyak di antaranya dapat diselesaikan dengan konsep himpunan. Agar dapat menyelesaikannya, Anda harus memahami kembali mengenai konsep diagram Venn dan Anda harus dapat menyatakan permasalahan…
  • Cara Menentukan Kelipatan Suatu Bilangan Bulat Positif Materi kelipatan suatu bilangan bulat positif merupakan materi dasar yang Anda harus kuasai untuk menguasai materi kelipatan persekutuan terkecil (KPK) yang akan kita bahas pada postingan berikutnya. Materi ini sudah…
  • Pengertian Peluang Usaha, Ciri, Faktor Yang… Pengertian Peluang Usaha, Ciri, Faktor Yang Mempengaruhi, Sumber dan Contoh Peluang Usaha Terlengkap – Istilah Peluang Usaha terdiri dari 2 (dua) kata yaitu kata Peluang dan kata Usaha. Peluang dapat diartikan…
  • Cara Mengerjakan Operasi Hitung Campuran Pada Bilangan Bulat Operasi hitung campuran pada bilangan bulat sering muncul pada soal-soal ujian nasional (UN). Jadi Anda sangat penting mengetahui cara mengerjakan operasi hitung campuran pada bilangan bulat. Contoh hitung campuran bilangan…
  • Rumus dan Cara Mencari Jumlah Tabungan Setelah dan Tahun Rumus dan cara mencari jumlah tabungan setelah n tahun perlu Anda ketahui karena hampir setiap UN soal-soal seperti itu sering keluar. Hanya saja bentuk soalnya sedikit dimodifikasi dan angkanya juga diubah,…
  • Menghitung Persentase Untung atau Rugi Dalam kehidupan sehari-hari kita sering mendengar kata “untung dan rugi”. Adakalanya dalam kehidupan sehari-hari untung atau rugi itu dinyatakan dalam bentuk persen. Biasanya persentase untung atau rugi dihitung dari harga…
  • Rumus Layang-Layang : Pengertian, Sifat, Menghitung… Rumus Luas dan Keliling Layang-Layang – Bangun layang-layang adalah? Apa rumus layang-layang? Sebutkan sifat-sifat layang-layang! Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian bangun layang-layang, sifat, gambar, rumus, contoh…
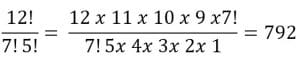
  • Cara Menentukan dan Menghitung Rumus Luas dan… Mengetahui Rumus hitung Luas dan Keliling Pada Trapesium Lengkap dengan Contoh Soal dan Pembahasannya Trapesium merupakan bangun datar dua dmensi yang dibentuk oleh empat buah rusuk yang dua diantara rusuknya…
  • Materi dan Soal Exercise Present Perfect Tense Kelas 9 SMP Materi dan Soal Exercise Present Perfect Tense Kelas 9 SMP - Hello everyone, how are you today? Pada kesempatan kali ini kami akan membahas mengenai salah satu tenses yaitu Present Perfect…
  • Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi… Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap dengan Cara Penyelesaiannya Pembahasan tentang Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal sudah kita bahas pada postingan…
Baca Juga :  Penyelesaian PLSV dengan Persamaan-Persamaan yang Ekuivalen
beherein.com
© Copyright 2022, All Rights Reserved