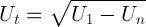Pengertian, Rumus & Contoh Soal Barisan Dan Deret Geometri Beserta Penjelasan Lengkap – Terdapat dua jenis Barisan dan Deret di dalam matematika yaitu Barisan dan Deret Aritmatika & Barisan dan Deret Geometri. Kali ini kita akan membahas tentang barisan dan deret geometri. Berikut adalah penjelasan selengkapnya:
Pengertian dan Rumus Barisan Geometri
Barisan Geometri dapat didefinisikan sebagai barisan yang tiap-tiap sukunya diperoleh dari hasil perkalian suku sebelumnya dengan sebuah konstanta tertentu.
Barisan geometri adalah barisan yang emmenuhi sifat hasil bagi sebuah suku dengan suku sebelumnya berurutan bernilai konstanta. Misalnya barisan geometri tersebut yaitu a,b, dan c maka c/b =b/a sama dengan konstanta. Hasil bagi suku yang berdekatan disebut disebut dengan rasio (r).
Misal ditemukan sebuah deret geometri
U1, U2, U3,…,Un-1, Un
Maka U2/U1, U3/U2,…, Un/Un-1 = r (konstan atau rasio)
Lalu bagaimana menentukan suku ke-n dari barisan geometri:
U3/U2 = r maka U3 = U2.r = a.r.r = ar2
Un/Un-1 = r maka Un = Un-1. r = arn-2.r = arn-2+1 = arn-1
jadi dapat disimpulkan bahwa rumus suku ke-n baris geometri yaitu Un = arn-1
a= suku awal r rasio
Contoh Barisan Geometri
Agar kalian lebih memahami apa yang dimaksud dengan barisan geometri. Perhatikan contoh berikut ini:
3, 9, 27 , 81, 243, …
Barisan di atas merupakan contoh barisan geometri dimana setiap suku pada barisan tersebut merupakan hasil dari perkalian suku sebelumnya dengan konstanta 3. Maka dapat disimpulkan bahwa rasio pada barisan di atas adalah 3. rasio pada suatu barisan bisa dirumuskan menjadi:
r = ak+1/ak
Dimana ak yaitu sembarang suku dari barisan geometri yang ada. sementara ak+1 yaitu suku selanjutnya setelah ak. Untuk menentukan suku ke-n dari sebuah barisan geometri, kita bisa menggunakan rumus sebagai berikut:
Un = arn-1
Dengan a merupakan suku awal dan r ialah nilai rasio dari sebuah barisan geometri.
Contoh Soal dan Pembahasan Barisan Geometri
1. Sebuah Bakteri mampu melakukan pembelahan diri menjadi 4 setiap 12 menit. berapakah jumlah bakteri yang ada setelah 1 jam jika sebelumnya terdapat 3 buah bakteri?
Cara penyelesaian:
Diketahui:
a = 3
r = 4
n = 1 jam/12 menit = 60/12 = 5
Ditanya: U5…?
Jawab:
Un = arn-1
U5 = 3 x 45-1
U5 = 3 x 256 = 768 bakteri
Pengertian dan Rumus deret Geometri
Deret geometri bisa diartikan sebagai jumlah dari n suku pertama pada sebuah barisan geometri. apabila suku ke-n dari suatu barisan geometri digambarkan dengan rumus: an = a1rn-1, maka deret geometrinya dapat dijabarkan menjadi:
Sn = a1 + a1r + a1r2 + a1r3 + … + a1rn-1
Jika kita mengalikan deret geometri di atas dengan -r, kemudian kita jumlahkan hasilnya dengan deret aslinya, maka kita akan memperoleh:
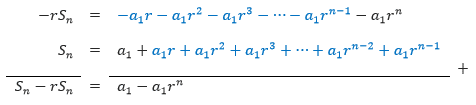
Setelah diperoleh Sn – rSn = a1 – a1rn maka kita bisa mengetahui nilai dari suku n pertama dengan cara sebagai berikut:
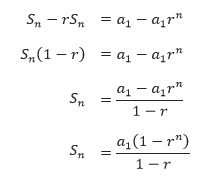
Berdasarkan kepada hasil perhitungan di atas, maka bisa disimpulkan bahwa rumus jumlan n suku pertama pada sebuah barisan geometri ialah:
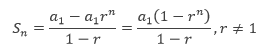
Contoh Soal Deret Geometri
1. Tentukanlah jumlah 8 suku pertama dari barisan geometri 2, 8, 32, ..
Cara penyelesaian:
Diketahui:
a = 2
r = 4
n = 8
Ditanya: S8..?
Sn = a (1-rn) / (1-r)
S8 = 2 (1-48) / (1-4)
S8 = 2 (1-65536)/ (-3)
S8 = 2 (-65535)/ (-3)
S8 = 2 x 21845
S8 = 43690
Sisipan Barisan Geometri
Dalam barsan geometri terdapat sisipa. Misalnya antara p dan q ada sisipan k buah bilangan dan terjadi barisan geometri, maka rasio barisan geometri dapat dicari dengan rumus:
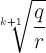
Suku Tengah Barisan Geometri
Apabila U1, U2,…,Un merupakan barisan geometri dengan n ganjil maka suku tengah barisan geometri tersebut dapat dicari dengan rumus berikut ini:
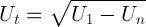
Deret Geometri Tak Hingga
Saat bola bekel dijatuhkan dari ketinggian 1 meter maka bola tersebut aka memantuk ketas sejauh 0,8 tinggi jatuh sebelumnya, lalu berapa jarak yang ditempuh bola bekel hingga berhenti?
Ini merupakan contoh deret geomerti tak hingga yaitu deret yang banyak sukunya tak terhingga. Jumlah suku dari deret tak hingga ada kemungkinan hingga atau tak hingga. Apabila deret tersebut hingga maka deret tersebut disebut deret konvergen dan Apabila tak hingga disebut deret divergen. Lebih jelasnya, apabila jumlah deret tak hingga menuju ke suatu harga tertentu yang berhingga maka disebut deret konvergen (mengerucut). Sebaliknya, deret geometri yang menuju bilangan tak hingga disebut deret divergen.
Deret tak hingga yang memilii rasio r ≥ 1 atau r ≤ 1 disebut deret divergen dan yang memiliki rasio -1< r < 1 disebut deret konvergen. Untuk menghitung deret tak hingga ada dua rumus tergantung pada nilai r.

Contoh Soal Deret Geometri Tak Hingga
1. Tentukan jumlah suku-suku deret geometri tak hingga dari 1 + 0,5 + 0,25 + 0,125 + …
Cara Penyelesaian:
Diketahui
a = 1
r = 0,5
Ditanya: S∞..?
S∞ = a/1-r
S∞ = 1/1-0,5
S∞ = 1/0,5
S∞ = 2
Demikian artikel pembahasan tentang”Pengertian, Rumus & Contoh Soal Barisan Dan Deret Geometri Beserta Penjelasan Lengkap“, semoga bermanfaat dan jangan lupa ikuti postingan kami berikutnya.
Artikel Paling Populer :
- Operasi Perpangkatan Pada Bentuk Aljabar pada postingan kali ini kami akan membahas tentang operasi perpangkatan pada bentuk aljabar. Operasi perpangkatan diartikan sebagai perkalian berulang dengan bilangan yang sama. Jadi, untuk sebarang bilangan bulat a, berlaku: Hal ini…
- Sejarah Suku Musi Banyuasin Musi Banyuasin adalah kelompok masyarakat asli yang bermukim di beberapa Kecamatan di Kabupaten Musi Banyuasin, Provinsi Sumatera Selatan, Kabupaten seluas 25.664 kilometer persegi ini terdiri atas 20 Kecamatan. Penduduk Kabupaten…
- Rumus Dan Contoh Soal Polinom atau Suku Banyak Dalam… Rumus Dan Contoh Soal Polinom atau Suku Banyak Dalam Matematika Perhatikan masalah yang di hadapi seorang peneliti sedang merancangsebuah wadah berbentuk balok dari bahan alumunium. Wadah tersebut harus mampu menampung…
- Rumus dan Cara Mencari Jumlah Tabungan Setelah dan Tahun Rumus dan cara mencari jumlah tabungan setelah n tahun perlu Anda ketahui karena hampir setiap UN soal-soal seperti itu sering keluar. Hanya saja bentuk soalnya sedikit dimodifikasi dan angkanya juga diubah,…
- Tabel Periodik Unsur Kimia : Pengertian, Gambar dan… Gambar Tabel Periodik Unsur Kimia – Unsur kimia adalah zat kimia yang tidak dapat diubah lagi menjadi zat yang kecil atau dapat juga diartikan zat yang tidak dapat dibagi lagi jika…
- Cabang-Cabang Matematika Cabang Matematika Cabang utama matematika adalah aljabar, teori bilangan, geometri dan aritmatika. Berdasarkan cabang-cabang ini utama ini cabang-cabang lain telah ditemukan. Sebelum munculnya zaman modern, studi matematika sangat terbatas. Namun seiring…
- Garis dan Sudut serta sifat-sifatnya Garis dan Sudut adalah bentuk dasar dalam geometri. Garis adalah gambar yang terdiri dari titik-titik tak terhingga yang membentang tanpa batas di kedua arah. Dengan kata lain, garis dibentuk oleh…
- Proporsi Proporsi Perbandingan/rasio dan proporsi merupakan dasar utama untuk memahami berbagai konsep dalam matematika maupun sains. Proporsi mengatakan bahwa dua perbandingan (atau dua pecahan) adalah sama. Dengan kalimat lain dua buah perbandingan dikatakan…
- Tabel Periodik Unsur Kimia adalah suatu susunan unsur-unsur berdasarkan urutan nomor atom dan kemiripan sifat unsur tersebut. Dinamakan periodik, sebagaimana terdapat pola kemiripan pada sifat unsur dalam susunan tersebut. Sistem periodic unsure (tabel periodik)…
- Penjumlahan dan Pengurangan Pada Bentuk Aljabar Operasi hitung pada bentuk aljabar sama seperti operasi hitung pada bilangan bulat yang meliputi: penjumlahan, pengurangan, perkalian, pembagian dan perpangkatan. Nah pada postingan ini kami hanya membahas tentang penjumlahan dan…
- Pengertian Kalimat Persuasif, Ciri Ciri dan Contoh… Pengertian Kalimat Persuasif , Ciri Ciri Kalimat Persuasif dan Contoh Kalimat Persuasif Terlengkap – Kalimat Persuasif adalah kalimat yang bertujuan untuk meyakinkan dan membujuk orang lain agar au mengikuti atau membeli suatu produk…
- Pengertian Dan Bentuk Lipatan Dan Patahan Beserta… Pengertian Dan Bentuk Lipatan Dan Patahan Beserta Macam Jenis Dan Contoh Lipatan dan Patahan Lengkap – Proses pembentukan kulit bumi yang tidak rata berupa gunung dan pegunungan, lembah, plato, dan retakan…
- Rumus Tabung : Volume, Luas Permukaan, Keliling,… Rumus Tabung : Volume, Luas Permukaan, Keliling, Tinggi dan Contoh Soal Tabung – Dalam matematika kita mempelajari tentang bangun ruang. Bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga…
- Bentuk dan Unsur - Unsur Aljabar Tahukah Anda apa pengertian aljabar (algebra)? Menurut Wikipedia, aljabar (algebra) berasal dari Bahasa Arab "al-jabr" yang artinya "hubungan" atau "penyelesaian". Jadi, aljabar merupakan cabang ilmu matematika yang mempelajari hubungan dan penyelesaian…
- Bola – Ciri, Contoh Soal Beserta Penyelesaian Luas… Bola – Ciri, Contoh Soal Beserta Penyelesaian Luas Permukaan dan Volume Bola Lengkap – Bola merupakan bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang…
- Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan… Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya Lengkap – Dalam matematika membahas tentang bangun ruang. Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk…
- Pegunungan Sirkum Pasifik dan Sirkum Mediterania Bumi kita memiliki 2 baris pegunungan utama yang membentuk barisan pegunungan-pegunungan besar. Kedua barisan pegunungan tersebut adalah sirkum pasifik yang mencakup wilayah Asia-Pasifik dan sirkum mediterania yang mencakup wilayah Asia-Eropa.…
- Pengertian Muatan Listrik, Jenis, Sifat, Rumus dan… Pengertian Muatan Listrik, Jenis, Sifat, Rumus dan Contoh Soal Muatan Listrik Lengkap – Muatan listrik adalah sifat atau muatan dasar yang dibawa partikel dasar sehingga menyebabkan partikel dasar tersebut mengalami gaya…
- Pengertian Gerak Epirogenetik dan Gerak Orogenetik… Pengertian Gerak Epirogenetik dan Gerak Orogenetik Dan Gambar Beserta Contohnya Lengkap – Tektonisme ialah proses perubahan letak lapisan bumi secara vertikal yang terjadi akibat pergerakan, pengankatan patahan dan lipatan pada struktur tanah di…
- Pengertian Alkana, Tata Nama, Sifat, Kegunaan dan… Pengertian Alkana, Tata Nama, Sifat, Kegunaan dan Contoh Alkana Terlengkap – Senyawa hidrokarbon adalah senyawa yang mengandung unsur hidrogen dan karbon. Atom karbon selain dapat membentuk rantai karbon, juga bisa…
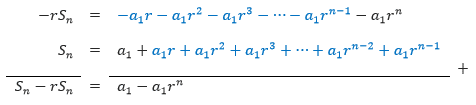
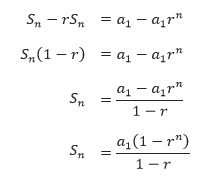
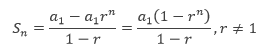
![]()