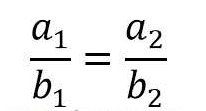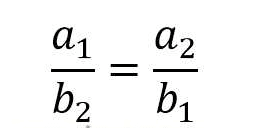Pengertian, Rumus, Contoh Soal Perbandingan Senilai dan Berbalik Nilai dan Penyelesaiannya Lengkap – Dalam matematika terdapat materi pembelajaran tentang perbandingan. Materi perbandingan termasuk ke dalam golongan aritmatika. Perbandingan adalah usaha membandingkan dua objek atau lebih dengan menggunakan rumus perbandingan yang tepat.
Terdapat 2 (dua) jenis perbandingan matematika yaitu perbandingan senilai dan perbandingan berbalik nilai. Perbandingan senilai memiliki nilai tetap yang sama, sedangkan perbandingan berbalik nilai memiliki nilai tetap meskipun terbalik.
Pengertian dan Rumus Perbandingan Senilai
Perbandingan senilai adalah cara membandingkan dua objek atau lebih dengan besar salah satu nilai veriabel yang bertambah maka membuat variabel lain menjadi bertambah juga. Untuk itu, perbandingan senilai memiliki jumlah nilai variabel yang sama. Misalnya jumlah barang dengan jumlah harga barang, jumlah nilai tabungan dengan waktu menyimpan, jumlah pekerja dengan gaji pekerja, dan lain sebagainya. Berikut rumus perbandingan senilai:
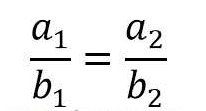
Dari rumus diatas dapat disimpulkan bahwa nilai a1 sama dengan nilai b1 dan nilai a2 sama dengan nilai b2.
Pengertian dan Rumus Perbandingan Berbalik Nilai
Perbandingan berbalik nilai adalah cara membandingkan dua objek atau lebih dengan besar nilai salah satu variabel yang berubah maka membuat variabel lain menjadi berkurang nilainya. Contohnya seperti jumlah hewan dengan waktu makanan habis, jumlah pekerja dan waktu pernyelesaian pekerjaan dan lain sebagainya. Berikut rumus perbandingan berbalik nilai:
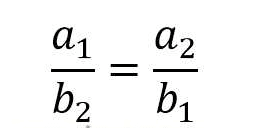
Dari rumus diatas, dapat disimpulkan bahwa nilai a1 berbalik nilai dengan b2 dan nilai a2 berbalik nilai dengan b1.
Contoh Soal Perbandingan Senilai dan Berbalik Nilai dan Penyelesaiannya
Berikut ini beberapa contoh soal perbandingan senilai dan perbandingan berbalik nilai:
1. Di pasar, 5 kg jeruk dijual dengan harga 60.000. Maka berapakah harga 10 kg jeruk?
Jawab:
Diketahui: a1 = 5; b1 = 60.000; a2 = 10
Ditanya: b2…?
Maka nilai b2
a1/b1 = a2/b2 (rumus perbandingan senilai)
5/60.000 = 10/b2 (Lakukan pengalian nilai secara menyilang)
5 x b2 = 10 x 60.000
b2 = 600.000/5
b2 = 120.000
Jadi harga 10 kg jeruk adalah Rp 120.000.
2. Pembangunan rumah dilakukan oleh 6 pekerja dengan waktu penyelesaian selama 20 hari. Jika jumlah pekerjanya menjadi 10 orang maka membutuhkan waktu berapa hari agar rumah tersebut selesai?
Jawab:
Diketahui: a1 = 6; b1 = 20; a2 = 10
Ditanya: b2…?
Maka nilai b2
a1/b2 = a2/b1 (rumus perbandingan berbalik nilai)
6/b2 = 10/ 20 (Lakukan pengalian nilai menyilang)
6 x 20 = 10 x b2
b2 = 120/10
b2 = 12
Jadi pekerja tersebut membutuhkan waktu selama 12 hari.
3. Pembuatan kolam renang dilakukan oleh 6 pekerja dengan gaji seluruh pekerja sebesar Rp 300.000. Tapi pemilik kolam renang ingin mempercepat pembuatannya, untuk itu ia menambahkan 2 orang lagi. Berapa jumlah gaji tambahannya?
Jawab:
Diketahui : a1 = 6; b1 = 300.000; a2 = 2
Ditanya : b2 = ?
Maka nilai b2
a1/b1 = a2/b2 (rumus perbandingan senilai)
6/300.000 = 2/b2 (Lakukan pengalian nilai menyilang)
6 x b2 = 300.000 x 2
b2 = 600.000/6
b2 = 100.000
Jadi jumlah gaji tambahannya yaitu sebesar Rp 100.000
4. Sebuah rumah dibangun dalam waktu 20 hari dengan jumlah pekerja 7 orang. Jika pemilik rumah tersebut ingin mempercepat waktunya menjadi 14 hari. Berapakah jumlah pekerja yang harus ditambah?
Jawab:
Diketahui: a1 = 20; b1 = 7; a2 = 14
Ditanya: b2…?
Maka nilai b2:
a1/b2 = a2/b1 (rumus perbandingan berbalik nilai)
20/b2 = 14/7 (Lakukan pengalian nilai menyilang)
20 x 7 = 14 x b2
b2 = 140/14
b2 = 10
Jadi pekerjanya harus ditambah sebanyak 10-7= 3 orang
5. Sebuah pabrik sepatu memiliki 5 mesin pembuat sepatu dengan waktu pembuatan 8 hari. Jika mesin yang digunakan berjumlah 8. Berapakah waktu yang dibutuhkan untuk membuat sepatu?
Jawab:
Diketahui : a1 = 5; b1 = 8; a2 = 8
Ditanya: b2…?
Maka nilai b2
a1/b2 = a2/b1 (rumus perbandingan berbalik nilai)
5/b2 = 8/8 (Lakukan pengalian nilai menyilang)
5 x 8 = 8x b2
b2 = 40/8
b2 = 5
Jadi waktu yang dibutuhkan selama 5 hari.
6. Perbandingan umur Dila dan adiknya adalah 1 : 3. Jumlah umur mereka 20 tahun. Berapakan umur Dila?
Jawab:
Diketahui:
Ani : Adik = 1 : 3
Jumlah umur Dila dan adiknya = 20 tahun
Ditanya: Umur Dila?
Jumlah perbandingan Ani dan adik = 1 + 3 = 4
Umur Ani = 1/4 x 20 tahun = 5 tahun
Demikian penjelasan yang bisa kami sampaikan tentang Pengertian, Rumus, Contoh Soal Perbandingan Senilai dan Berbalik Nilai dan Penyelesaiannya Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Artikel Paling Populer :
- Pengertian Gerak Vertikal ke Bawah, Ciri, Rumus dan… Pengertian Gerak Vertikal ke Bawah (GVB), Ciri, Rumus dan Contoh Soal Gerak Vertikal ke Bawah Beserta Pembahasan Lengkap – Gerak Vertikal ke Bawah (GVB) adalah salah satu bentuk gerak lurus yang…
- Pengertian Superlative, Bentuk dan Contohnya Terdapat beraneka ragam ungkapan yang biasa dipakai ketika sedang melakukan percakapan sehari-hari, mulai dari ungkapan tentang kebahagiaan, kesedihan, perhatian, pendapat dan yang lainnya. Dalam situasi itulah yang pada akhirnya harus…
- Pengertian, Rumus dan Contoh Soal Mol, Molalitas,… Pengertian, Rumus dan Contoh Soal Menghitung Mol, Molalitas, Molaritas, Normalitas, Part Per Million (ppm), Persen Massa dan Persen Volume Larutan Lengkap – Dalam kimia, ada beberapa satuan yang sering digunakan untuk…
- Pengertian, Rumus dan Contoh Soal Mol, Molalitas,… Pengertian, Rumus dan Contoh Soal Menghitung Mol, Molalitas, Molaritas, Normalitas, Part Per Million (ppm), Persen Massa dan Persen Volume Larutan Lengkap – Dalam kimia, ada beberapa satuan yang sering digunakan untuk…
- 5 Contoh Soal Kimia Dan Pembahasan Terlengkap… Telah kita pelajari tentang pengertan termokimia pada postingan sebelumnya. Bahwa Termokimia adalah cabang ilmu kimia yang mempelajari tentang perubahan kalor atau energi yang menyertai suatu reaksi kimia, baik yang diserap…
- Gagasan Besar Pecahan Pecahan memiliki pembilang dan penyebut. Penyebut memberi tahu berapa banyak bagian yang sama dari keseluruhan yang dibagi dan pembilang memberi tahu berapa banyak bagian yang ada. Pecahan dapat memiliki arti…
- Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi… Soal Dan Pembahasan Fungsi Komposisi, Aljabar Fungsi dan Komposisi Fungsi Lengkap dengan Cara Penyelesaiannya Pembahasan tentang Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal sudah kita bahas pada postingan…
- Pengertian Pola Bilangan : Macam Jenis dan Contoh… Pengertian Pola Bilangan : Macam Jenis dan Contoh Pola Bilangan Sebelum mempelajari barisan aritmatika dan barisan geometri, ada sub bab materi barisan bilangan atau bab yang perlu dipahami terlebih dahulu yaitu pola…
- Elastisitas Fisika – Pengertian, Rumus, Hukum Hooke,… Elastisitas Fisika : Pengertian, Rumus, Hukum Hooke, Dan Contoh Soal – Pada kendaraan bermotor, baik mobil ataupun sepeda motor, dipasang sistem alat yang berfungsi untuk meredam kejutan. Sistem alat ini dinamakan…
- Pecahan sebagai Perbandingan Bagian dari Keseluruhan Kita ketahui bahwa pecahan merupakan bagian dari keseluruhan (silahkan baca pengertian bilangan pecahan). Misalnya sebuah apel dibagi menjadi dua bagian yang sama, maka setengah buah apel merupakan bagian dari satu buah…
- Materi Lengkap Trigonometri Dengan Fungsi , Rumus… Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal Dalam merancang kerangka sebuah jembatan perhitungan yang dilakukan tidaklah mudah. Beban, tegangan, serta gaya yang bekerja pada jembatan menjadi…
- Pengertian, Jenis-Jenis dan Contoh Soal Pesawat… Pengertian, Jenis-Jenis dan Contoh Soal Pesawat Sederhana Beserta Pembahasan Lengkap – Pesawat sederhana adalah semua alat bantu yang susunannya sederhana dan bisa memudahkan pekerjaan manusia. Pesawat sederhana ini memberikan banyak keuntungan…
- Pengertian Produktivitas Kerja, Pengukuran dan… Pengertian Produktivitas Kerja, Pengukuran dan Faktor Yang Mempengaruhi Produktivitas Kerja Lengkap – Produktivitas kerja adalah kemampuan karyawan dalam berproduksi dibandingkan dengan input yang digunakan, seorang karyawan bisa dikatakan produktif jika ia…
- Pengertian Konjungsi Subordinatif, Jenis dan Contoh… Pengertian Konjungsi Subordinatif, Jenis dan Contoh Konjungsi Subordinatif Lengkap – Konjungsi subordinatif adalah kata penghubung yang menghubungkan dua buah frasa, klausa, atau kalimat yang berkedudukan tidak setara atau tidak sederajat.…
- Molaritas, Molalitas, Normalitas, Fraksi Mol Ada yang sudah mengenal atau pernah mendengar mengenai Molaritas, Molalitas, Normalitas, dan Fraksi Mol? 1. Mol Larutan (n) Mol merupakan massa (gram) pada suatu zat dibagi dengan massa molekul relatif atau berat…
- Cara menghitung Gambar atau Model Berskala Jika kalian Anda menggambar jarak antara dua kota pada kertas gambar, apakah Anda dapat menggambarkannya dengan ukuran yang sebenarnya? Tentu tidak bukan? Untuk hal seperti inilah Anda perlu mempelajari mengenai…
- Pengertian massa jenis Zat Pada postingan ini akan membahas salah satu besaran turunan yaitu massa jenis. Apa pengertian massa jenis? Sebelumnya kami sudah membahas mengenai besaran turunan. Salah satu contoh besaran turunan adalah massa jenis. Kenapa…
- Penerapan Pertidaksamaan Linear Satu Variabel Untuk mengerjakan soal-soal pertidaksamaan linear satu variabel yang berkaitan dengan permasalahan dalam kehidupan sehari-hari caranya hampir sama seperti mengerjakan soal-soal persamaan linear satu variabel (Silahkan baca penerapan persamaaan linear satu variabel).…
- Pengertian Radiasi Benda Hitam Dan Radiasi Panas… Pengertian Radiasi Benda Hitam Dan Radiasi Panas Beserta Rumus Dan Contoh Soal Lengkap – Pernahkah kalian memakai baju hitam pada siang hari? Jika pernah melakukannya, bagaimana rasanya? Pasti sangat panas, bukan?…
- Pengertian Gaya Berat, Rumus dan Contoh Soal Gaya… Pengertian Gaya Berat, Rumus dan Contoh Soal Gaya Berat Beserta Cara Penyelesaiannya Terlengkap – Dalam kehidupan sehari-hari, kita sering menggunakan gaya berat salah satu contohnya adalah saat kita menimbang barang.…