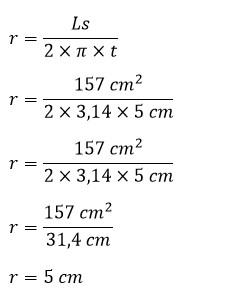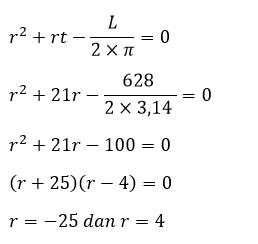Rumus Tabung : Volume, Luas Permukaan, Keliling, Tinggi dan Contoh Soal Tabung – Dalam matematika kita mempelajari tentang bangun ruang. Bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya.
Ada 7 macam jenis bangun ruang, salah satunya adalah tabung. Apa itu bangun tabung? agar lebih memahaminya, kali ini kita akan membahas rumus tabung mulai dari rumus volume tabung, rumus keliling tabung, menghitung luas tabung hingga mengetahui rumus tabung tanpa tutup, berikut selengkapnya:
Pengertian Bangun Tabung
Bangun Tabung adalah sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk sebuah lingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang. Tabung juga disebut dengan silinder.
Ada banyak benda berbentuk tabung yang kita temui di kehidupan sehari-hari seperti gelas, kaleng susu, drum, botol, seruling dan lain sebagainya. Berikut gambar bangunan tabung:
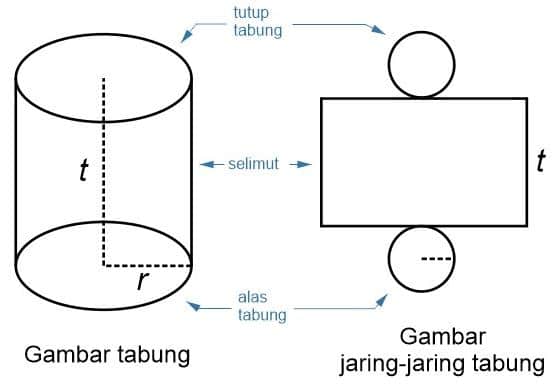
Sifat Sifat Bangun Tabung
Ciri ciri tabung diantaranya yaitu:
- Memiliki 2 (dua) buah rusuk lengkung.
- Memiliki alas dan tutup berbentuk lingkaran yang masing-masing sama besar.
- Memiliki 3 (tiga) buah sisi diantaranya dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.
- Tidak memiliki titik sudut
Jenis-Jenis Tabung
Ada 2 jenis tabung yaitu
Tabung Tertutup
Tabung Tertutup adalah sebuah tabung yang seluruh bidang dan sisi – sisinya tertutup.
Tabung Terbuka
Tabung Terbuka adalah sebuah tabung yang salah satu sisi alasnya atau sisi atapnya terbuka dan bahkan keduanya antara sisi alas dan sisi atapnya juga terbuka.
Rumus Menghitung Luas dan Volume Tabung
Rumus Tabung
Secara singkat rumus tabung yaitu:
Keliling Alas Tabung = 2πr
Volume Tabung (V) = πr²t
Luas Tabung (L) = 2πr²
Keterangan:
V = Volume tabung(cm3)
π = 22/7 atau 3,14
r = Jari – jari /setengah diameter (cm)
t = Tinggi (cm)
Rumus Luas Permukaan Tabung
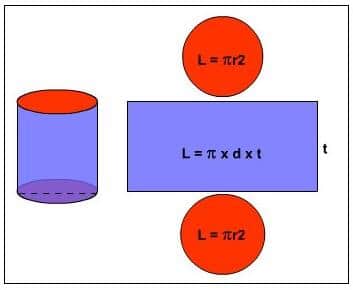
Luas permukaan tabung adalah suatu luas dari beberapa jumlah sisi yang dimiliki tabung. Jumlah sisi suatu tabung sama dengan bidang pembentuk tabung. Bidang pembentuknya terdiri dari dua buah lingkaran yang menjadi alas dan tutupnya, dan satu buah selimut tabung yang berbentuk persegi panjang. Luas permukaan ini memiliki pengaruh terhadap besar dan kecilnya suatu tabung.
Untuk rumus luas permukaan tabung bisa dicari menggunakan sebuah jaring-jaring tabung. Jaring-jaring tabung tersebut terdiri dari
Tutup dan atas tabung yang berbentuk lingkaran dengan besar jari-jari (r), sehingga rumus luas lingkaran = 2πr². Untuk jari-jarinya bisa menggunakan π= 22/7 atau 3,14.
Bagian lengkungannya berbentuk persegi pajang dengan panjang tabung memiliki rumus keliling alas tabung yaitu 2πr serta bagian lebar tabung yang memiliki rumus luas 2πrt.
Berdasarkan ulasan rumus luas tabung tersebut, maka dapat disimpulkan:
Rumus luas tutup serta alas tabungnya yaitu πr² + πr² = 2πr²
Rumus luas selimut tabung yaitu p (keliling alas) x l (tinggi tabung) = 2πr x t = 2πrt
Maka, rumus luas permukaan tabung yaitu = Luas tutup + alas + selimut tabung = 2πr²+2πrt = 2πr(r+t)
Rumus Luas Permukaan Tabung Tanpa Tutup
Luas permukaan tabung tanpa tutup adalah suatu luas permukaan yang hampir sama dengan luas permukaan tabung, hanya berbeda pada segi tutupnya saja, luas permukaan tanpa tutup tabung ini tidak ada tutupnya. Karena tidak memiliki tutup, maka luas sisi tutup tabung yang berupa lingkaran tersebut tidak dihitung.
Rumus luas tutup tabung : 2πr
Rumus luas alas tabung : 2πr
Rumus luas selimut tabung : 2πr²t
Karena tanpa tutup, maka rumus luas permukaan tabung tanpa tutup bisa disimpulkan sebagai berikut:
Luas tabung tanpa tutup = π x r2 + 2 x π x r x t = π x r (r + 2t)
Rumus Volume Tabung
Rumus volume tabung adalah perkalian antara tinggi dengan luas alas tabung. Bangun tabung memiliki sebuah alas dan tutup yang berbentuk lingkaran, untuk itu untuk menghitung volumenya cukup mengalikan tinggi dengan luas alasnya saja. Berikut rumus volume tabung:
Volume Tabung = πr²t
Rumus Keliling Alas Tabung
Karena alas tabung berbentuk lingkaran, maka rumus keliling alas tabung yaitu:
Keliling alas = 2πr
Rumus Luas Jaring-Jaring Tabung
L = alas x tinggi = a x t
Rumus Gabungan Kerucut
Selain rumus-rumus diatas ada juga rumus gabungan antara tabung dengan bangun lainnya seperti gabungan tabung dan kerucut, gabungan tabung dan setengah lingkaran, serta gabungan tabung dan lingkaran . Berikut ini rumus gabungannya:
Rumus gabungan kerucut dan tabung
Rumus volume gabungan tabung dan kerucut yaitu ( π.r².t )+( 1/3.π.r².t )
Rumus luas gabungan tabung dan kerucut yaitu (π.r²)+(2.π.r.t)+(π.r.s)
Rumus gabungan tabung dan setengah bola
Rumus volume gabungan tabung dan setengah bola yaitu π.r².t+2/3. π.r3
Rumus luas gabungan tabung dan setengah bola (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)
Rumus gabungan tabung dan bola
Rumus volume gabungan tabung dan bola yaitu (π.r².t)+(4/3. π.r3)
Rumus luas gabungan tabung dan bola yaitu (2. π.r²)+(4. π.r²) = π.r²
Contoh Soal Tabung dan Pembahasannya
Contoh Soal Volume Tabung
Contoh Soal 1
Berapakah volume sebuah tabung yang memiliki sebuah diameter 60 cm dan tinggi 70 cm?
Jawab :
diameter = 60 cm, karena r = 1/2 diameter maka r = 30 cm
tinggi = 70 cm
Volume Tabung = π x r² x t
= (22/7) x 30² x 70
= (22/7) x 30 x 30 x 70
= (22/7) x 63000
= 198.000 cm³.
Contoh Soal 2
Seorang tukang kayu memotong sebuah kayu menjadi sebuah tabung atau silinder dengan luas penampang alasnya adalah 250 cm². Tabung atau silinder dari kayu tersebut memiliki tinggi 35 cm. Hitunglah volume tabung atau silinder dari kayu tersebut:
Jawab :
Volume silinder = luas penampang alas atau lingkaran x tinggi
Volume silinder kayu = 250 cm² x 35 cm = 8750 cm³.
Maka, volume silinder tersebut adalah 8750 cm³.
Contoh Soal 3
Seorang penjual minyak memiliki sebuah drum berbentuk tabung yang ia gunakan untuk menyimpan minyak dagangannya. Jari-jari alas yang dimiliki drum itu adalah 70cm dan memiliki tinggi 100cm. Berapa liter minyak yang dapat ditampung dalam drum tersebut?
Jawab : V = π r² x tinggi
V = 22/7 x 70² x 100
V = 1.540.000 cm³ = 1. 540 dm3 = 1.540 liter
Jadi dapat disimpulkan bahwa jumlah minyak yang mampu ditampung dalam drum tersebut sebanyak 1.540 liter.
Contoh Soal Luas Permukaan Tabung
Contoh Soal
Sebuah tabung memiliki diameter dan tinggi yang masing masing ukurannya yaitu 20 dan 16. Berapakah Luas permukaan yang dimiliki tabung tersebut?
Jawab :
Diketahui:
d = 20, r= 10
t = 16
Jawab:
Rumus luas permukaan tabung = 2πr(r+t)
2πr(r+t)
=2 × 22/7× 10 (10 + 16)
=1634,28
Contoh Soal Luas Selimut Tabung
Contoh Soal
Apabila diketahui sebuah tabung yang memiliki r = 14 dan tinggi 30. Tentukanlah luas selimut tabung tersebut:
Jawab :
Rumus luas selimut tabung : 2πrt
= 2 × 22/7 × 14 × 30
= 2 x 1320
= 2640
Contoh Soal Keliling Alas Tabung
Apabila ada sebuah tabung yang diketahui memiliki jari- jari yaitu 18 cm. Carilah dan hitunglah keliling alas tabung tersebut:
Penyelesaian :
Diketahui :
r = 18 cm
Ditanya : K = …?
Jawab :
K = 2 x π x r
K = 2 x 22/7 x 18
K = 792 / 7
K = 113.14 cm
Maka, keliling alas tabung tersebut adalah 113.14 cm
Contoh Soal Luas Permukaan Tabung Tanpa Tutup
Diketahui sebuah tabung berdiameter 20 cm dengan tinggi tabung adalah 24 cm. Berapakah luas permukaan tabung tanpa tutup tersebut?
Jawab:
Rumus luas permukaan tabung tanpa tutup = π x r (r + 2t)
= 3,14 x 10 x (10 x 2 x 24)
= 3,14 x 10 x (10 x 48)
= 3,14 x 10 x 480
= 15.072 cm2
Jadi, luas permukaan tabung tanpa tutup adalah 15.072 cm2
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Volume Tabung
Contoh Soal
Hitunglah jari-jari tabung yang memiliki tinggi 8 cm dan volume 2512 cm³!
Diketahui:
t = 8 cm
V = 2512 cm³
Ditanya:
Jari-jari tabung (r)
Pembahasan:
Jadi, jari-jari tabung adalah 10 cm.
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Luas Selimut
Contoh Soal
Hitunglah jari-jari tabung yang mempunyai tinggi 5 cm dan luas selimut 157 cm²!
Diketahui:
t = 5 cm
Ls = 157 cm
Ditanya:
Jari-jari tabung (r)
Pembahasan:
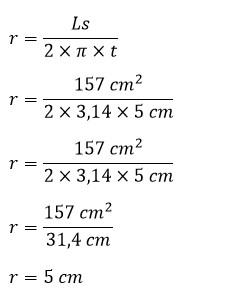
Jadi, jari-jari tabung adalah 5 cm.
Contoh Soal Menghitung Jari-Jari Tabung Jika Diketahui Luas Permukaan
Contoh Soal
Hitunglah jari-jari tabung yang mempunyai tinggi 21 cm dan luas permukaan 628 cm²!
Diketahui:
t = 21 cm
L = 628 cm²
Ditanya:
Jari-jari tabung (r)
Penyelesaian:
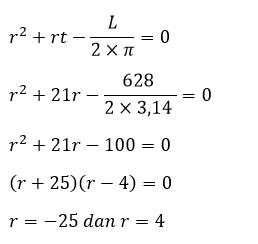
Jari-jari tabung memenuhi persamaan berikut
Dari hasil faktor persamaan dapat diuji
r = -25 cm tidak memenuhi syarat, karena hasil luas permukaan akan bernilai negatif atau tidak sama 628 cm².
r = 4 cm memenuhi syarat, karena hasil hasil luas permukaan bernilai 628 cm².
Jadi, jari-jari tabung tersebut adalah 4 cm.
Artikel Paling Populer :
- Pengertian, Rumus dan Contoh Soal Mol, Molalitas,… Pengertian, Rumus dan Contoh Soal Menghitung Mol, Molalitas, Molaritas, Normalitas, Part Per Million (ppm), Persen Massa dan Persen Volume Larutan Lengkap – Dalam kimia, ada beberapa satuan yang sering digunakan untuk…
- Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan… Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya Lengkap – Dalam matematika membahas tentang bangun ruang. Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk…
- Pengertian Gaya Berat, Rumus dan Contoh Soal Gaya… Pengertian Gaya Berat, Rumus dan Contoh Soal Gaya Berat Beserta Cara Penyelesaiannya Terlengkap – Dalam kehidupan sehari-hari, kita sering menggunakan gaya berat salah satu contohnya adalah saat kita menimbang barang.…
- Suhu – Pengertian Termometer, Jenis , Pengukurannya… Pada saat matahari terbit dari timur, tubuh kita akan merasakan kehangatan. Suasana yang tadinya gelap menjadi terang dan aktivitas pun segera dimulai. Apakah yang menyebabkan tubuh kita merasa hangat? Mengapa…
- Pengertian, Bunyi, Rumus, Penerapan dan Contoh Soal… Pengertian, Bunyi, Rumus, Penerapan dan Contoh Soal Hukum Pascal Terlengkap – Hukum Pascal berbunyi: “jika tekanan yang diberikan pada satu bagian zat cair dalam suatu ruangan tertutup, maka akan diteruskan oleh…
- Tekanan Udara: Pengertian, Faktor, dan Cara Mengukurnya Udara disekitar kita memiliki berat, semakin banyak udara yang ada di atas kita, maka semakin berat pula udara yang kita rasakan. Hal ini kerap dikenal dengan istilah tekanan udara atau air…
- Cermin Cekung : Pengertian, Sinar Istimewa, Sifat… Cermin Cekung: Pengertian, Sinar Istimewa, Sifat Bayangan, Rumus dan Contoh Soal Cermin Cekung Terlengkap – Cermin cekung merupakan cermin yang berbentuk lengkung, dimana permukaan cermin cekung yang memantulkan cahaya melengkung…
- Penerapan Pertidaksamaan Linear Satu Variabel Untuk mengerjakan soal-soal pertidaksamaan linear satu variabel yang berkaitan dengan permasalahan dalam kehidupan sehari-hari caranya hampir sama seperti mengerjakan soal-soal persamaan linear satu variabel (Silahkan baca penerapan persamaaan linear satu variabel).…
- Cara Menentukan dan Menghitung Rumus Luas dan… Mengetahui Rumus hitung Luas dan Keliling Pada Trapesium Lengkap dengan Contoh Soal dan Pembahasannya Trapesium merupakan bangun datar dua dmensi yang dibentuk oleh empat buah rusuk yang dua diantara rusuknya…
- Pengertian, Rumus & Contoh Soal Barisan Dan Deret… Pengertian, Rumus & Contoh Soal Barisan Dan Deret Geometri Beserta Penjelasan Lengkap – Terdapat dua jenis Barisan dan Deret di dalam matematika yaitu Barisan dan Deret Aritmatika & Barisan dan…
- Pengertian Pola Bilangan : Macam Jenis dan Contoh… Pengertian Pola Bilangan : Macam Jenis dan Contoh Pola Bilangan Sebelum mempelajari barisan aritmatika dan barisan geometri, ada sub bab materi barisan bilangan atau bab yang perlu dipahami terlebih dahulu yaitu pola…
- Teori Kinetik Gas – Persamaan Umum Gas, Hukum Gas… Pernahkah Anda melihat gelembung-gelembung ketika minuman bersoda dituangkan? Bagaimana bentuk dan jumlahnya? Gelembung-gelembung minuman bersoda merupakan inti molekul-molekul. Gelembung-gelembung minuman bersoda akan berjumlah banyak dan volumenya semakin membesar saat dituangkan.…
- Rumus dan Cara Mencari Jumlah Tabungan Setelah dan Tahun Rumus dan cara mencari jumlah tabungan setelah n tahun perlu Anda ketahui karena hampir setiap UN soal-soal seperti itu sering keluar. Hanya saja bentuk soalnya sedikit dimodifikasi dan angkanya juga diubah,…
- Pengukuran Suhu Suhu adalah ukuran panas dan dinginnya suatu benda.Suhu diukur dengan bantuan alat yang disebut termometer. Tiga satuan suhu yang digunakan adalah Celcius, Fahrenheit, dan Kelvin. Setiap makluk hidup dapat merasakan…
- Pengertian, Rumus dan Contoh Soal Mol, Molalitas,… Pengertian, Rumus dan Contoh Soal Menghitung Mol, Molalitas, Molaritas, Normalitas, Part Per Million (ppm), Persen Massa dan Persen Volume Larutan Lengkap – Dalam kimia, ada beberapa satuan yang sering digunakan untuk…
- Mengenal Fungsi Epididimis sebagai Sarana… Setiap makhluk hidup memiliki alat untuk reproduksi, termasuk manusia. Laki-laki dan perempuan memiliki organ reproduksi yang berbeda, begitu pula dengan fungsinya. Sistem reproduksi sendiri merupakan sistem biologis yang terdiri dari…
- Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus… Balok – Sifat-Sifat Balok, Unsur-Unsur Balok, Rumus dan Contoh Soal Balok Beserta Cara Penyelesaian – Balok adalah bangun ruang 3 dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling…
- Sentriol Adalah Ada yang sudah mengenal atau pernah mendengar mengenai istilah Sentriol? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Sentriol Sentriol merupakan salah satu bagian sebuah organel sel yang terdiri dari dua…
- Penjelasan Lengkap Sistem Peredaran Darah Pada Manusia Anemia sel sabit ditandai dengan sel-sel darah merah yang berbentuk seperti bulan sabit atau seperti huruf C. Sel darah merah yang normal berbentuk bulat seperti donat tanpa lubang dan di…
- Pemuaian – Pengertian, Jenis , Rumus Dan Contoh Soal LENGKAP Benda-benda pada umumnya akan memuai pada saat dipanaskan. Akan tetapi, ada beberapa manfaat dari pemuaian, antara lain pengelingan pelat logam pada pembuatan badan kapal, keping bimetal yang dimanfaatkan pada sakelartermal,…