Pengertian, Penjelasan Lengkap Tentang Konsep didalam Logika Matematika Disertai Contoh
Logika matematika merupakan salah satu materi pelajaran matematika yang merupakan gabungan dari ilmu logika dan ilmu matematika. Logika berasal dari bahasa yunani kuno yaitu λόγος (logos), logos dapat diartikan sebagai hasil pertimbangan akal atau pikiran yang dinyatakan lewat kata atau bahasa. Sedangkan jika diartikan secara sistematis, logika dapat dianalisis berdasarkan nilai-nilai kebenaran.
Logika matematika merupakan salah satu ilmu matematika yang banyak diaplikasikan dalam kehidupan sehari-hari. Seperti contohnya dalam kepolisian, ilmu ini digunakan untuk menganalisis kasus sedangakan dalam dunia komputer ilmu logika matematika diterapkan sebagai media penarik kesimpulan.
Dalam logika matematika, terdapat beberapa tahap yang dibahas, antara lain pernyataan, negasi , disjungsi , konjungsi , implikasi , biimplikasi,dua pernyataan yang ekuivalen, kalimat berkuantor, serta penarikan kesimpulan. Simak untuk mengetahui lebih jelas materi tentang logika matematika dibawah ini:
1. Pernyataan
Pernyataan yaitu kalimat yang mempunyi nilai benar atau salah, tetapi dengan pernyataan keduanya (Benar-salah). Sebuah kalimat tidak dapat ditentukan sebagai pernyataan apabila kita tidak bisa menentukan kebenaran atau kesalahan dan bersifat relatif. Dalam logika matematika terdapat dua jenis pernyataan, yaitu pernyataan tertutup dan pernyataan terbuka.
Pernyataan tertutup adalah kalimat pernyataan yang sudah bisa dipastikan nilai benar/salah nya.
pernyataan terbuka adalah kalimat pernyataan yang belum dapat dipastikan nilai benar/salah nya.
Contoh :
- 2 X 4 = 8 (Sudah pasti benar / Pernyataan tertutup)
- 15 : 5 = 5 (Sudah pasti salah / Pernyataan tertutup)
- Gula putih rasanya manis (Harus dibuktikan dahulu / Pernyataan terbuka)
- Jarak antara Bogor dan Bekasi adalah dekat (Pernyataan relatif)
2. Negasi
Negasi atau Ingkaran merupakan pernyataan yang isinya mengingkari pernyataan atau berisi kalimat sangakalan, negasi biasanya dibentuk dengan cara menambahkan kata “tidak benar bahwa” pada awal kalimatnya atau memberikan simbol ” ~” pada awal pernyataannya.
Contoh:
- Pernyataan 1
- Bumi itu Bulat
- Pernyataan 2
- Tidak benar bahwa Bumi itu bulat.
3. Konjungsi
Konjungsi yaitu pernyataan majemuk yang dihubungkan dengan kata hubung “dan” atau disimbolkan dengan “^”. Pernyataan konjungsi hanya memiliki nilai benar jika kedua pernyataan di dalamnya bernilai benar. Jika salah satu pernyataan bernilai salah, maka pernyataan konjungsi juga bernilai salah.
Perhatikan tabel kesimpulan :

4. Disjungsi
Disjungsi adalah pernyatan majemuk yang dihubungkan dengan kata “atau” yang disimbolkan dengan “V” . Disjungsi merupakan kebalikan dari konjungsi. Pernyataan disjungsi hanya akan bernilai salah jika kedua pernyataan yang terdapat didalamnya bernilai salah. Jika salah satu pernyataan bernilai benar, maka pernyataan disjungsi juga bernilai benar.
Perhatikan tabel dibawah ini.

5. Implikasi
Implikasi yaitu pernyataan majemuk yang diawali dengan kata jika dan dihubungkan dengan kata hubung “maka” yang disimbolkan dengan “=>”. Misal “p => q” dibaca “p maka q”.
Perhatikan tabel dibawah ini

6. Biimplikasi
Biimplikasi yaitu bentuk kompleks sari implikasi yang berarti “jika dan hanya jika” yang disimbolkan dengan “<=>”. Misal p <=> q dibaca “p jika dan hanya jika q”.
Perhatikan tabel dibawah ini.

7. Ekuivalensi Pernyataan Majemuk
Ekuivalensi pernyataan majemuk yaitu persesuaian yang bisa diterapkan dalam konsep-taan majemuk yang telah dijelaskan diatas, dengan metode ini kita dapat mengetahui negasi dari konjungsi, disjungsi, implikasi dan juga biimplikasi. Konsep ekuivalensi dinyatakan dalam rumus-rumus tertentu, seperti rumus berikut ini.
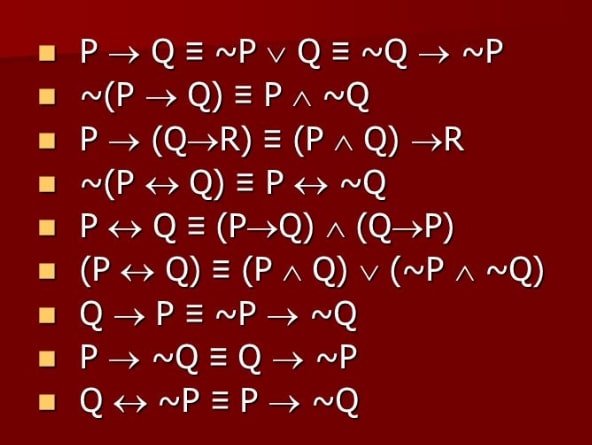
8. Konvers
Konvers merupakan kebalikan dari implikasi yaitu ditandai dengan pertukaran letak. Misalkan “p => q” , maka koners nya adalah “q => p”.
9. Invers
Invers adalah lawan dari implikasi. Dalam invers, pernyataan yang terdapat pada pernyataan majemuk merupakan negasi dari pernyataan pada implikasi. Misal p => q, maka inversnya adalah ” ~p => ~q”
10. Kontraposisi
Sementara kontraposisi merupakan kebalikan daripada invers sama halnya dengan konvers, hanya pernyataan majemuknya merupakan negasi atau ingkaran. Misalkan invers “~p => ~q” . Maka kontraposisi nya adalah “~q => ~p”
11. Kuantor Pernyataan
Pernyataan kuantor yaitu bentuk pernyataan yang didalamnya terdapat konsep kuantitas. terdapat dua jenis kuantor, yaitu kuantor universal dan kuantor eksistensial.
- Kuantor universal digunakan dalam pernyataan yang menggunakan konsep setiap atau semua
![]()
- Kuantor eksistensial digunakan dalam pernyataan yang mengandung konsep ada, sebagian, beberapa, atau terdapat.
![]()
12. Ingkaran dari pernyataan berkuantor
Pernyataan berkuantor memiliki negasi atau ingkaran. Negasi dari berkuantor universal adalah kuantor eksistensial begitu juga sebaliknya. Perhatikan contoh berikut.
- p : beberapa mahasiswa memiliki semangat belajar yang tinggi
- ∼p : semua mahasiswa tidak memiliki semangat belajar yang tinggi
13. Penarikan Kesimpulan
Kesimpulan dapat dilakukan dari beberapa pernyataan yang diketahui nilai kebenarnya yang disebut premis. Kemudian dengan menggunakan prinsip-prinsip yang ada diperoleh pernyataan yang baru yang disebut kesimpulan/konklusi yang diturunkan dari premis yang ada. Penarikan kesimpulan seperti itu sering disebut dengan argumentasi. Suatu argumentasi dikatakan sah Jika premis-premisnya benar maka konklusinya juga benar. Terdapat 3 metode dalam penarikan kesimpulan, yaitu : Modus ponens, Modus Tolens, dan Silogisme.
Perhatikan Contoh Berikut.
- Modus ponens
premis 1 : p →q
premis 2 : p ( modus ponens)
__________________
Kesimpulan: q
Arti Modus Ponens adalah “jika diketahui p → q dan p, maka bisa ditarik kesimpulan q“.
sebagai contoh :
premis 1 : Jika paman datang ke desa adik akan merasa senang
premis 2 : Paman tidak datang
__________________
Kesimpulan: Adik tidak merasa senang
- Modus Tollens
premis 1 : p →q
premis 2 : ~q ( modus tollens)
__________________
Kesimpulan: ~p
Modus Tollens berarti “jika diketahu p → q dan ~q, maka bisa ditarik kesimpulan ~p“.
sebagai contoh :
premis 1 : Jika hari hujan, maka aku memakai payung
premis 2 : Aku memakai payung
___________________
Kesimpulan : Hari hujan
- Silogisme
premis 1 : p→q
premis 2 : q → r ( silogisme)
_________________
Kesimpulan: p →r
Silogisme berarti “jika diketahu p → q dan q→r, maka bisa ditarik kesimpulan p→r“.
sebagai contoh :
Premis 1 : Jika harga BBM naik, maka harga bahan pokok naik.
Premis 2 : Jika harga bahan pokok naik maka semua orang tidak senang.
__________________________________________________
Kesimpulan: Jika harga BBM naik, maka semua orang tidak senang.
Dengan diberikannya materi logika matematika, diharapakan dapat membantu dan menambah wawasan para pembaca khususnya dalam pelajaran matematika. Semoga artikel ini bermanfaat, sampai bertemu dipostingan selanjutnya…