Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal

Pengertian, Sifat Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal

Sebuah produk massal biasanya dibuat melalui beberapa proses. Proses-proses tersebut ditangani oleh mesin-mesin yang berbeda. Urutan pengerjaan produk tersebut tentu tidak boleh tertukar. Sebagai contoh, pada sebuah pabriksirop, mesin pencuci buah digunakan terlebih dahulu sebelum mesin pengupas buah digunakan. Begitu seterusnya hingga sirop dikemas.

Prinsip yang sama berlaku pada komposisi fungsi. Dalam bahasa yang mudah, komposisi fungsi adalah operasi penyusunan beberapa fungsi dengan aturan tertentu sehingga terbentuk fungsi baru. Urutan penggabungan fungsi akan berpengaruh terhadap komposisi fungsi yang dihasiikan. Sebagai catatan, jika hasii komposisi fungsi berupa fungsi, hasil komposisi fungsi itu disebut fungsi komposisi.

Agar lebih paham, simaklah uraian mengenai fungsi, sifat fungsi, serta sifat-sifat komposisi fungsi berikut.

Fungsi dan Sifat-sifatnya

1. Pengertian Fungsi

Suatu relasi dikatakan sebagai fungsi jika setiap unsur di daerah asai (domain = D) dipasangkan dengan tepat ke satu unsur di daerah kawan. Sebagai misal A dan B masing-masing merupakan himpunan. Reiasi fungsi (f) dari A ke B (f: A → B) dikatakan sebagai fungsi jika setiap anggota A dipasangkan dengan tepat ke satu anggota B.

2. Sifat-Sifat Fungsi

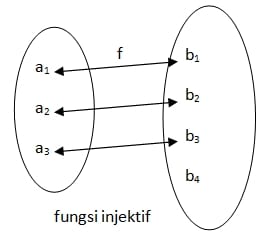
Fungsi Injektif (Fungsi Satu-Satu)
Fungsi f dari A ke B merupakan fungsi injektif jika anggota B dipasangkan dengan tepat ke satu anggota A, tetapi tidak semua anggota B harus mempunyai pasangan dengan anggota A. Dengan kata lain, fungsi f dari A ke B merupakan fungsi injektif jika a₁ , a₂ € D_f dengan a₁ ≠ a₂ maka f(a₁) ≠ f(a2). Df = daerah asal fungsi f.

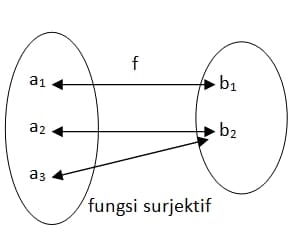
Fungsi surjektif (Fungsi onto)
Fungsi f dari A ke B merupakan fungsi surjektif jika setiap anggota B mempunyai pasangan dengan anggota A.

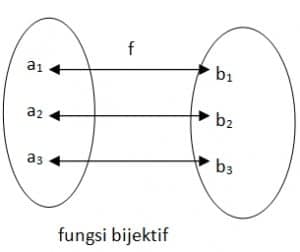
Fungsi Bijektif (Fungsi Berkorespondensi Satu-Satu)
Suatu fungsi dikatakan bijektif jika fungsi tersebut merupakan fungsi injektif sekaligus surjektif.

Aljabar Fungsi

1. Penjumlahan, Pengurangan, Perkalian, dan Pembagian Dua Fungsi

Jika f dan g merupakan fungsi, berlaku sifat-sifat aijabar fungsi sebagai berikut.

Penjumlahan fungsi : (f + g)(x) = f(x) + g(x)
Pengurangan fungsi: (f – g)(x) = f(x) – g(x)
Perkalian fungsi : (f . g)(x) = f(x) . g(x)
Pembagian fungsi : (^f/_g) (x) = ^f(x)/_g(x) . g(x) ≠ 0

2. Daerah Asal Fungsi

Diketahui f dan g merupakan fungsi dengan D_f = daerah asal f dan D_g = daerah asal g. Daerah asal operasi aljabar dua fungsi sebagai berikut.

Daerah asal fungsi (f + g)(x): D_{f + g} = Df ∩ Dg
Daerah asal fungsi (f – g)(x): D_{f -g} = Df ∩ Dg
Daerah asal fungsi (f . g)(x) : D_f.g = Df ∩ Dg
Daerah asal fungsi (^f/_g) (x) : D_f/g = Df ∩ Dg dengan g(x) 0

Komposisi Fungsi

1. Pengertian Komposisi Fungsi

Jika f dan g merupakan fungsi, komposisi fungsi f dan g (ditulis f ₒ g) dirumuskan sebagai berikut.

(f ₒ g)(x) = f(g(x))

f ₒ g dibaca f bundaran g atau f komposisi g.
Artinya, mula-mula unsure x € D_g dipetakan oleh g ke g(x), kemudian g(x) dipetakan oleh f ke f(g(x)). Dengan cara yang sama diperoleh komposisi fungsi berikut.

(g ₒ f)(x) = g(f(x))
(f ₒ g ₒ h)(x) = f(g(h(x)))

2. Sifat-Sifat Komposisi Fungsi

Komposisi fungsi tidak bersifat komutatif.
(f ₒ g)(x) ≠ (g ₒ f)(x)
Komposisi fungsi bersifat asosiatif.
(f ₒ g ₒ h)(x) – (f ₒ (g ₒ h))(x) = ((f ₒ g) ₒ h)(x)
Dalam komposisi fungsi terdapat sebuah fungsi identitas, yaitu |(x) = x sehingga (f ₒ l)(x) = (I ₒ f)(x) = f(x)

Demikian penjelasan yang bisa kami sampaikan tentang Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal. Semoga postingan ini bermanfaat bagi pembaca . Sampai jumpa pada postingan selanjutnya.

Artikel Paling Populer :

Pengertian DNA dan RNA, Fungsi, Struktur dan… Pengertian DNA dan RNA, Fungsi, Struktur dan Jenisnya Terlengkap – Kali ini kita akan membahas tentang DNA (Deoxyribonucleic acid) dan RNA (Ribonucleic acid), serta fungsi, struktur atau komponen penyusun dan jenisnya lengkap.…
Pengertian Piramida Penduduk : Fungsi, Macam Bentuk… Pengertian Piramida Penduduk – Apa yang dimaksud dengan piramida penduduk? Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian piramida penduduk, fungsi, ciri dan macam bentuk piramida penduduk secara…
Suatu cara yang memiliki fungsi untuk mematikan dan… Suatu cara yang memiliki fungsi untuk mematikan dan menutup semua program perangkat komputer adalah... A. Sleep B. Restart C. Turn off D. Update E. Shutdown Jawaban : E. Shutdown
Materi Stoikiometri Ada yang sudah mengenal atau pernah mendengar mengenai Stoikiometri? Oke, mari simak penjelasan secara lengkapnya dibawah ini ya. Pengertian Stoikiometri Kata “Stoikiometri” ini berasal dari bahasa Yunani, yaitu dari kata “Stoicheion” yang berarti “unsur” dan juga…
Perangkat lunak yang memiliki fungsi utama sebagai… Perangkat lunak yang memiliki fungsi utama sebagai pengolah kata adalah... A. Recycle bin B. Blender C. Photoshop D. Webster E. Microsoft Word Jawaban : E. Microsoft Word
Pengertian Surat Edaran, Fungsi, Jenis, Bagian dan… Pengertian Surat Edaran, Fungsi, Jenis, Bagian dan Contoh Surat Edaran Terlengkap – Surat edaran adalah surat yang berisi pemberitahuan resmi dalam instansi, lembaga atau organisasi. Atau lebih jelasnya, definisi surat edaran…
Pengertian Router, Fungsi, Jenis dan Cara Kerja… Pengertian Router, Fungsi, Jenis dan Cara Kerja Router Lengkap – Router, Perute atau Penghala adalah perangkat keras jaringan komputer yang bisa digunakan untuk menghubungkan beberapa jaringan yang sama atau berbeda.…
Rumus Perhitungan, Penjumlahan, Pengurangan,… Rumus Perhitungan, Penjumlahan, Pengurangan, Pembagian, Perkalian di Excel Dan Contohnya Terlengkap Hal dasar yang harus kita kuasi dalam belajar excel adalah mengetahui operasi perhitungan matematika, seperti operasi hiutng penjumlahan, pengurangan,…
Sebuah komposisi warna termudah untuk menyeimbangkan… Sebuah komposisi warna termudah untuk menyeimbangkan visualisasi atau biasa disebut dengan color matching adalah... A. RGB color B. Primary color C. Secondary color D. Tertiary color E. Monochromatic Jawaban :…
Tombol ini memiliki fungsi untuk menggerakan kursor… Tombol ini memiliki fungsi untuk menggerakan kursor satu layar ke bawah, disebut... A. Tab B. Page down C. Page up D. Esc E. Back space Jawaban : B. Page down
Pengertian Otak Besar , Fungsi, Struktur dan Bagian… Pengertian Otak Besar , Fungsi, Struktur dan Bagian Otak Besar (Cerebrum) Terlengkap – Otak besar atau cerebrum merupakan masa embrionik, sistem saraf pusat membentuk kanal pusat yang dangkal ventrikel dan membentuk…
Apa Contoh Bahan Kimia Sebagai Pemutih Pernahkah anda mencuci baju dengan deterjen tetapi nodanya masih menempel pada baju. Apa yang anda lakukan agar noda tersebut lenyap di baju? Cara yang paling mudah menghilangkan noda baju adalah dengan menggunkan…
Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan… Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan Tata Nama Senyawa Kimia Beserta Contohnya Lengkap – Senyawa kimia adalah zat kimia murni yang terdiri dari dua atau beberapa unsur yang bisa…
Cara Menggunakan Fungsi SUMIF dan SUMIFS pada Excel… Cara Menggunakan Fungsi SUMIF dan SUMIFS pada Excel Lengkap dengan Rumus dan Contohnya Pada postingan sebleumnya, kita telah membahas tentang kegunaan masing-masing dari microsoft Office. Salah satu nya yaitu Microsoft Excel.…
25 Fungsi Hati Manusia Sebagai Organ Tubuh… Inilah Fungsi Hati dalam Organ Tubuh yang Memiliki Fungsi Paling Penting untuk Manusia Hati atau Liver merupakan salah satu organ yang ada dalam tubuh manusia, organ ini merupakan kelenjar terbesar…
Kimia Analisis Ada yang sudah mengenal atau pernah mendengar mengenai istilah Kimia Analisis? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Kimia Analisis Kimia Analisis merupakan salah satu cabang ilmu Kimia yang mempelajari…
Pengertian HUB, Fungsi, Jenis-Jenis, Kelebihan dan… Pengertian HUB, Fungsi, Jenis-Jenis, Kelebihan dan Kekurangan HUB Lengkap – Hub atau pusatan Ethernet adalah sebuah peranti jaringan komputer yang berfungsi untuk menghubungkan peranti-peranti dengan kabel Ethernet atau serat optik agar…
Pengertian Diensefalon, Fungsi, Struktur dan… Pengertian Diensefalon, Fungsi, Struktur dan Bagian-Bagian Diensefalon Terlengkap – Diensefalon (Diencephalon) merupakan istilah yang digunakan untuk menyatakan struktur disekitar ventrikel ke 3 (tiga) dan membentuk inti serebrum atau otak besar. Anggota…
Sebutkan fungsi dari perangkat keras! Sebutkan fungsi dari perangkat keras! Jawab : Input divice berfungsi sebagai media untuk memasukan data dari luar ke dalam memori prosessor untuk menghasilkan informasi. - Process device berfungsi untuk memproses…
Jelaskan fungsi dari sistem operasi Resource Manager! Jelaskan fungsi dari sistem operasi Resource Manager! Jawab : Resource Manager adalah sebuah aplikasi yang merupakan bawaan windows yang berfungsi untuk menampilkan sumber daya yang terpakai pada komputer, diantaranya seperti…

Baca Juga : Penerapan Persamaan Linear Satu Variabel