Pengertian dan Cara Menyajikan Relasi dalam Matematika

Pengertian dan Cara Menyajikan Relasi dalam Matematika

Salam jumpa kembali dengan artikel-artikel portal yang selalu menyajikan informasi seputar materi pelajaran dan pengetahuan umum. Kali ini kita akan membahas salah satu ilmu matematika yang mungkin sudah anda pelajari dalam lingkungan sekolah. Untuk kalian yang masih berada dikelas VIII, mungkin materi ini sudah ada pelajari, Materi tersebut yaitu Relasi dalam matematika. Masih ingatkah kalian dengan pengertian dari Relasi? Oke baiklah.. akan kami ingatkan kembali. Untuk mengetahui lebih lengkapnya, simak ulasan selanjutnya…

Pengertian Relasi

Relasi merupakan suatu aturan yang memasangkan anggota himpunan ke himpunan lain. Relasi dari himpunan A ke himpunan B adalah menghubungkan anggota-anggota himpunan A dengan anggota-anggota himpunan B.
Lebih lengkapnya perhatikan contoh berikut ini.

Diketahui jika himpunan A = {Rani, Rina, Rini, Rana} , himpunan B ={MTK, IPA, IPS},maka relasi yang didapat adalah “suka dengan mata pelajaran” .

Dalam menyajikan suatu relasi kita dapat menyatakannya melalui 3 cara, yaitu dengan Diagram Panah, Diagram Cartesius, dan Himpunan pasangan. Untuk mengetahui lebih jelasnya simak ulasan dibawah ini.

Diagram Panah

Diagram panah merupakan diagram yang menunjukkan relasi, yaitu relasi pelajaran yang disukai dari himpunan A dan himpunan B. Arah dari panah menunjukkan anggota-anggota himpunan A yang berelasi dengan anggota-anggota tertentu himpunan B.

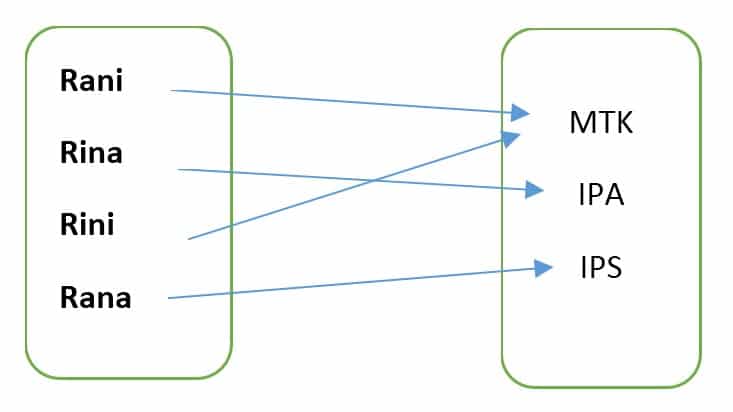
diagram-panah

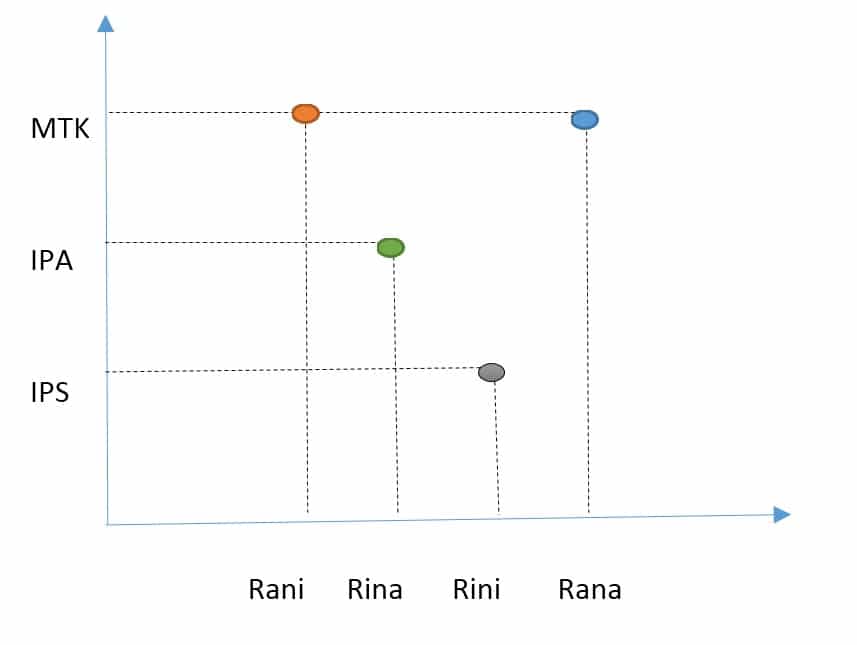
Diagram Cartesius

Pada diagram cartesius masih memiliki relasi dari diagram diatas. Perhatiakan diagram dibawah, pada anggota-anggota dari himpunan A berada pada sumbu mendatar sedangkan anggota-anggota dari himpunan B berada pada sumbu tegak. Selanjutnya setiap pasangan anggota himpunan A yang berelasi dengan anggota himpunan B kita nyatakan menggunakan titik atau noktah.

diagram-cartesius

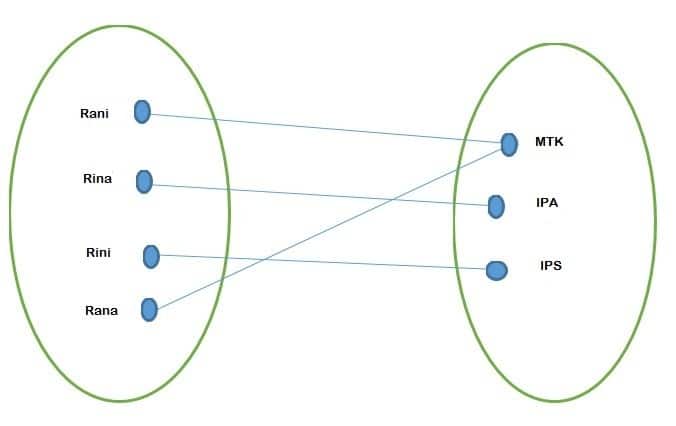
Himpunan Pasangan

Berdasarkan kasus diatas, kita dapat menyatakan himpunan pasangan berurutan dengan memasangkan secara berurutan anggota-anggota himpunan A dan himpunan B, yaitu :

{(Rani,MTK) , (Rina,IPA) , (Rini,IPS) , (Rana,MTK)}

himpunan-persamaan

Sifat-Sifat Relasi

Sebuah relasi A×A, yaitu relasi dari himpunan A kepada A sendiri, dapat memiliki sifat-sifat berikut:

  • Refleksif
    • Sebuah relasi R dalam A disebut memiliki sifat refleksif, jika setiap elemen A berhubungan dengan dirinya. Contoh relasi yang memiliki sifat seperti ini adalah relasi “x selalu bersama y.”, dengan x dan y adalah anggota himpunan seluruh manusia. Jelas sekali bahwa setiap orang pasti selalu bersama dengan dirinya sendiri.
  • Irefleksif
    • Relasi R dalam A disebut memiliki sifat irefleksif, jika setiap elemen A tidak berhubungan dengan dirinya sendiri. Contoh relasi irefleksif adalah relasi “x mampu mencukur rambut y dengan rapi sempurna.”, dengan x dan y adalah setiap pemotong rambut. Diandaikan bahwa setiap orang hanya dapat mencukur rambut orang lain dengan rapi sempurna, maka relasi ini adalah irefleksif, karena tidak ada seorang tukang cukur a yang mampu mencukur rambutnya sendiri. Contoh lain dalam himpunan bilangan bulat adalah, relasi < dan > adalah irefleksif.
  • Simetrik
    • Relasi R dalam A disebut memiliki sifat simetrik, jika setiap pasangan anggota A berhubungan satu sama lain. Dengan kata lain, jika a terhubung dengan b, maka b juga terhubung dengan a. Jadi terdapat hubungan timbal balik. Sebuah relasi “ genap” adalah relasi simetrik, karena untuk sembarang x dan y yang kita pilih, jika memenuhi relasi tersebut, maka dengan menukarkan nilai y dan x, relasi tersebut tetap dipenuhi. Misalnya untuk pasangan (5, 3) relasi tersebut dipenuhi, dan untuk (3, 5) juga.
  • Anti-simetrik
    • Jika setiap a dan b yang terhubung hanya terhubung salah satunya saja (dengan asumsi a dan b berlainan), maka relasi macam ini disebut relasi anti-simetrik.
  • Transitif
    • Sebuah relasi disebut transitif jika memiliki sifat, jika a berhubungan dengan b, dan b berhubungan dengan c, maka a berhubungan dengan c secara langsung. Sebagai contoh, relasi dua transitif. Misalnya untuk 5, 6, dan 7, berlaku 5 < 6, 6 < 7, dan 5 < 7

Dengan diberikannya materi Jenis jenis Satuan Hitung Dalam Ilmu Matematika , diharapkan dapat membantu dan menambah wawasan para pembaca khususnya dalam pelajaran matematika. Semoga artikel ini bermanfaat, sampai bertemu dipostingan selanjutnya…

Artikel Paling Populer :

  • Materi dan Soal Bahasa Inggris 'Government' Kelas 6 SD Pada kesempatan kali ini kami akan membahas tentang materi government atau dalam bahasa indonesianya adalah pemerintahan. Di suatu tempat tinggal atau daerah pasti memiliki sebuah struktur kenegaraan yang diisi mulai…
  • Pengertian Bilangan Bulat Masih ingatkah Anda dengan bilangan cacah? Bilangan cacah sudah Anda pelajari pada saat duduk di bangku sekolah dasar. Coba Anda ingat kembali materi tersebut! Adapun bilangan cacah yaitu 0, 1,…
  • Materi Bahasa Inggris Describing People and Object… Hello everyone, how are you today? Pada kesempatan kali ini kami akan membahas tentang materi bahasa inggris describing people and object bagi murid SD Kelas 6. Penting sekali bagi kalian…
  • Rumus Dan Pembahasan Contoh Soal Persamaan Lingkaran… Rumus Dan Pembahasan Contoh Soal Persamaan Lingkaran Matematika  Lingkaran adalah tempat kedudukan atau himpunan titik titik yang berjarak sama terhadap suatu titik tertentu. Titik tertentu tersebut dinamakan pusat lingkaran dan…
  • Materi 'Things at School' beserta Contoh Kalimat… Hello everyone, how are you today? Pada kesempatan kali ini kami akan membahas materi things at school atau bahasa indonesianya adalah barang barang yang ada di sekolah. Mari kita bagi…
  • 15 Contoh Soal Dan Pembahasan Materi Peluang… 15 Contoh Soal Dan Pembahasan Materi Peluang Kejadian Matematika Setelah kita bahas tentang peluang kejadian pada postingan sebelumnya, kali ini kita bahas tentang Contoh soal dan pembahasan materi peluang matematika.…
  • Menyajikan Operasi Himpunan dalam Diagram Venn Kalian telah mempelajari cara membaca diagram Venn. Sekarang, kita akan mempelajari cara menyajikan suatu himpunan ke dalam diagram Venn. Misalkan S = {1, 2, 3, ..., 10}, P = {1, 3, 5,…
  • Trik Rahasia Belajar Hitung Cepat Matematika Dengan… Inilah Trik Rahasia Belajar Hitung Cepat Matematika Dengan Mudah dan Menyenangkan  Pengalaman pribadi penulis, kalau sudah bertemu mata pelajaran matematika rasanya ingin cepat pulang, hehe.. semoga pembaca semua tidak seperti…
  • Materi dan Soal Bahasa Inggris Expressing Politeness… Hello para jagoan bahasa inggris, bertemu lagi dengan kami disini. Pada kesempatan kali ini kami akan membahas tentang bagaimana menyatakan atau menanyakan hal dengan cara yang lebih sopan dalam bahasa…
  • Himpunan berhingga, tak berhingga, kosong dan Semesta Pada postingan sebelumnya telah Anda ketahui bahwa banyaknya anggota himpunan A dinyatakan dengan n(A). Jika suatu himpunan dinyatakan dengan mendaftar anggota-anggotanya maka kalian dapat menentukan banyaknya anggota himpunan tersebut. Jika A adalah himpunan bilangan…
  • Rumus dan Cara Mencari Jumlah Tabungan Setelah dan Tahun Rumus dan cara mencari jumlah tabungan setelah n tahun perlu Anda ketahui karena hampir setiap UN soal-soal seperti itu sering keluar. Hanya saja bentuk soalnya sedikit dimodifikasi dan angkanya juga diubah,…
  • Sifat-Sifat Operasi Himpunan Sifat-sifat irisan dan gabungan himpunan Kalian telah mempelajari bahwa anggota irisan dua himpunan adalah anggota persekutuan himpunan tersebut. Jika A = {1, 2, 3, 4}, B = {3, 4, 5}…
  • Menentukan Banyaknya Himpunan Bagian dari Suatu Himpunan Anda telah mempelajari cara menentukan himpunan bagian suatu himpunan yang memiliki satu anggota, dua anggota, tiga anggota, dan n anggota. Untuk mengetahui banyaknya himpunan bagian suatu himpunan, pelajari tabel berikut. Himpunan Banyaknya Anggota Himpunan…
  • Fungsi Komposisi, Aljabar Fungsi Dan Komposisi… Pengertian, Sifat Fungsi Komposisi, Aljabar Fungsi Dan Komposisi Fungsi Matematika Disertai Rumus Soal Sebuah produk massal biasanya dibuat melalui beberapa proses. Proses-proses tersebut ditangani oleh mesin-mesin yang berbeda. Urutan pengerjaan produk…
  • Materi 'Foods and Drinks' beserta Lagu dan Soal Latihannya Hello para Jagoan Bahasa Inggris, bertemu lagi dengan kami disini. Pada kesempatan kali ini kami akan membahas Materi Foods and Drinks yang berarti makanan dan minuman. Hmmm, yummy! eitsss, tapi…
  • Cara Cepat Menentukan Periode dan Golongan Unsur Kami akan memberikan pengetahuan mengenai cara cepat menentukan periode dan golongan unsur. Kalian tau kan materi ini adalah materi pelajaran kimia tentang tabel periodik unsur. Ini referensi buat kalian supaya…
  • Pengertian Bilangan, Macam-Macam Bilangan dan… Pengertian Bilangan, Macam-Macam Jenis Bilangan dan Contohnya Lengkap – Kali ini kita akan membahas tentang pengertian bilangan dan macam-macam jenis bilangan beserta contoh bilangannya. Pengertian Bilangan Bilangan adalah suatu konsep matematika…
  • Hubungan Antar Himpunan Setelah mempelajari mengenai himpunan dan cara menyatakan suatu himpunan pada postingan sebelumnya, pada postingan ini kalian akan mempelajari hubungan antarhimpunan. Sekarang perhatikan contoh dua himpunan berikut ini ! A = {burung, ayam, bebek} dan…
  • Materi dan Soal Exercise Asking for Repetition Kelas 9 SMP Materi dan Soal Exercise Asking for Repetition Kelas 9 SMP - Hello para Jagoan Bahasa Inggris, bertemu lagi dengan kami disini. Pada kesempatan ini kami akan membahas mengenai salah satu expression…
  • Sintaksis Adalah Ada yang sudah mengenal atau pernah mendengar mengenai istilah Sintaksis? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Sintaksis Kata sintaksis ini berasal dari Yunani, yakni “sun” serta “tatein”, yang memiliki…
Baca Juga :  Pengertian dan Cara Menentukan Pecahan Senilai
beherein.com
© Copyright 2022, All Rights Reserved