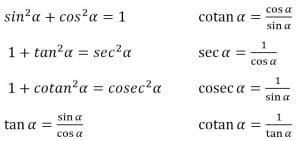Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal

Dalam merancang kerangka sebuah jembatan perhitungan yang dilakukan tidaklah mudah. Beban, tegangan, serta gaya yang bekerja pada jembatan menjadi pertimbangan utama para perancang untuk mengonstruksikan model rancangannya. Proses ini didasarkan atas pengetahuan dari bangsa Romawi bahwa busur dapat menjangkau jarakyang lebih jauh dan menahan berat yang lebih berat daripada lintel (bentuk balok yang lurus horizontal). Atas dasar ini semakin banyak pula jembatan berbentuk busur yang dibangun. Penggunaan bentuk busur ini melibatkan kelengkungan yang perlu diperhitungkan kemiringan sudutnyayang diberikan dalam persamaan trigonometri. Lebih lanjut mengenai persamaan trigonometri akan Anda pelajari pada uraian berikut.

A. Perbandingan Trigonometri

Perhatikan lingkaran dengan pusat O (0, 0) dan jari-jari (r), sedangkan titik A (x, y) pada lingkaran dan sudut dibentuk oleh OA terhadap sumbu X. Pada berlaku r² = x² + y² sehingga diperoleh perbandingan trigonometri sebagai berikut.

1. Rumus Jumlah dan Selisih dua Sudut

a. Rumus untuk Cosinus jumlah selisih dua sudut

cos (A + B) = cos A cos B – sin A sin B cos
(A – B) = cos A cos B + sin A sin B

b. Rumus untuk Sinus Jumlah dan Selisih Dua Sudut

sin (A + B) = sin A cos B + cos A sin B sin
(A – B) = sin A cos B – cos A sin B

c. Rumus untuk Tangen Jumlah dan Selisih Dua Sudut

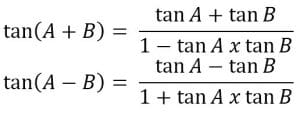
Contoh Soal

Jika tan 5°= p tentukan tan 50°

Jawab :

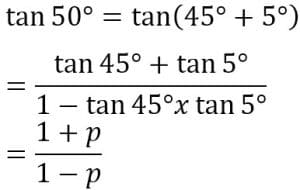
2. Rumus Trigonometri untuk sudut rangkap

a. Dengan menggunakan rumus sin (A+ B) untuk A = B, maka diperoleh:

sin 2A = sin (A + B)
= sin A cos A + cos A sin A
= 2 sin A cos A
Jadi,sin2A =2 sin A cos A

b. Dengan menggunakan rumus cos (A + B) untuk A = B, maka diperoleh:

cos 2A = cos (A + A)
= cos A cos A-sin A sin
A = cos²A-sin2A ……………(1)

Atau

Cos 2A = cos²A-sin²A
= cos² A- (1 – cos² A)
= cos² A – 1 + cos² A
= 2 cos² A – 1 ……….(2)

Atau

Cos 2A = cos²A-sin²A
= (1 -sin²A)-sin²A
= 1 – 2 sin²A ………. (3)

Dari persamaan (1) (2) (3) didapatkan rumus sebagai berikut.

Cos 2A = cos² A – sin² A
= 2 cos² A-1
= 1 – 2 sin² A

c. Dengan menggunakan rumus tan (A+B) untuk A=B, diperoleh

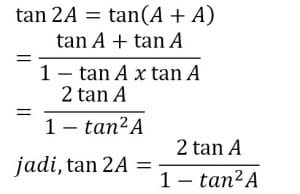
B. Perkalian, Penjumlahan, dan Pengurangan Sinus dan Kosinus

a. Rumus Perkalian Sinus dan Kosinus

2 sin A sin B = cos (A- B) – cos (A+ B)
2 sin A cos B = sin (A + B) + sin (A-B)
2 cos A sin B = sin (A + B)-sin (A-B)
2 cos A cos B = cos (A + B) + cos (A- B)

Contoh Soal

Tentukan nilai dari: 2 cos 75° cos 15°

Jawab:

2 cos 75° cos 15° = cos (75 +15)° + cos (75 – 15)°
= cos 90° + cos 60°
= 0 + ½
= ½

b.Rumus Penjumlahan dan Pengurangan Sinus dan Kosinus

sin A + sin B = 2sin ½ (A+B) cos ½ (A-B)
sin A – sin B = 2cos ½ (A+B) sin ½ (A-B)
cos A + cos B = 2cos ½ (A+B) cos ½ (A-B)
cos A – cos B = -2sin ½ (A+B) cos ½ (A-B)
tan A + tan B =
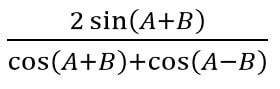
tan A – tan B =

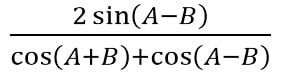
Contoh Soal

Tentukan nilai dari sin 105° + sin 15°

jawab:

sin 105° + sin 15° = 2 sin ½ (105+15)°cos ½ (105-15)°
= 2 sin ½ (102)° cos ½ (90)°
= sin 60° cos 45°

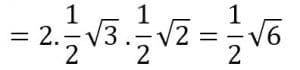
C. Identitas Trigonometri

Rumus rumus dasar identitas trigonometri sebagai berikut.

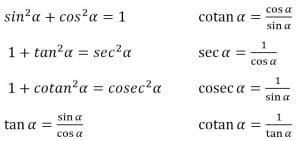
Untuk membuktikan suatu persamaan mempakan identitas atau bukan maka persamaan itu diubah dengan salah satu dari cara-cara berikut.

Mengubah bentuk ruas kiri sehingga menjadi bentuk ruas kanan.
Mengubah bentuk ruas kanan, sehingga menjadi bentuk ruas kiri.
Mengubah bentuk ruas kiri maupun ruas kanan sehingga menjadi bentuk yang sama.

Contoh Soal

Buktikan bahwa sin⁴ α – sin² α = cos⁴ α – cos² α

Jawab.

sin⁴ α – sin² α = (sin²α)² – sin² α
= (1 cos² α)²– (1 cos² α)
= 1 – 2 cos² α + cos⁴ α – 1 + cos² α
= cos⁴ α – cos² α

Demikian penjelasan yang bisa kami sampaikan tentang Materi Lengkap Trigonometri Dengan Fungsi , Rumus Dan Pembahasan Contoh Soal. Semoga postingan ini bermanfaat bagi pembaca dan bisa dijadikan sumber literatur untuk mengerjakan tugas. Sampai jumpa pada postingan selanjutnya.

Artikel Paling Populer :

Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan… Rumus Kerucut : Pengertian, Ciri, Sifat, Unsur dan Contoh Soalnya Lengkap – Dalam matematika membahas tentang bangun ruang. Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk…
Sifat Cermin Cembung Pengertian Cermin Cembung Cermin cembung merupakan sebuah cermin yang memiliki bentuk lengkung, yang di mana permukaan cermin nya yang memantulkan suatu cahaya yang melengkung ke luar. Cermin cembung juga memiliki…
Pembahasan Lengkap Aturan Cosinus Segitiga… Pembahasan Lengkap Aturan Cosinus Segitiga Trigonometri Dalam Ilmu Matematika – Teorema Pythagoras merupakan suatu rumus matematika yang sangat penting dalam geometri. Dengan menggunakan teorema phytagoras, kita bisa menghitung jarak antara dua…
Penyelesaian Persamaan Linear Satu Variabel Bentuk Pecahan Dalam menyelesaikan persamaan linear satu variabel (PLSV) yang berbentuk pecahan caranya hampir sama seperti mengerjakan PLSV yang bentuknya bukan pecahan yang sudah dibahas pada postingan sebelumnya dan tetnunya cara tersebut hampir sama…
Bilangan Pangkat Pecahan : Pengertian, Rumus, Sifat… Bilangan Berpangkat Pecahan : Pengertian, Rumus, Sifat Operasi Hitung dan Contoh Soal Bilangan Pangkat Pecahan Lengkap – Bilangan berpangkat adalah bentuk perkalian bilangan-bilangan yang sama atau perkalian berulang, pangkat pada bilangan…
Pengertian Muatan Listrik, Jenis, Sifat, Rumus dan… Pengertian Muatan Listrik, Jenis, Sifat, Rumus dan Contoh Soal Muatan Listrik Lengkap – Muatan listrik adalah sifat atau muatan dasar yang dibawa partikel dasar sehingga menyebabkan partikel dasar tersebut mengalami gaya…
Pengertian Getaran, Macam Jenis, Rumus, dan Contoh… Pengertian Getaran, Macam Jenis, Rumus, dan Contoh Soal Getaran Lengkap – Getaran adalah peristiwa bolak balik secara teratur suatu benda melalui atu titik seimbang. Karena terjadi dengan teratur, getaran juga sering disebut dengan gerak…
Menghitung Persentase Untung atau Rugi Dalam kehidupan sehari-hari kita sering mendengar kata “untung dan rugi”. Adakalanya dalam kehidupan sehari-hari untung atau rugi itu dinyatakan dalam bentuk persen. Biasanya persentase untung atau rugi dihitung dari harga…
Pengertian, Sifat, Rumus dan Contoh Soal Tekanan… Pengertian, Sifat, Rumus dan Contoh Soal Tekanan Hidrostatis Beserta Pembahasan Terlengkap – Tekanan hidrostatis adalah tekanan yang diakibatkan oleh gaya yang ada pada zat cair terhadap suatu luas bidang tekan…
Pengertian, Rumus dan Contoh Soal Listrik Dinamis… Pengertian, Rumus dan Contoh Soal Listrik Dinamis Beserta Cara Penyelesaian Lengkap – Listrik dinamis (electronidinamic) berasal dari perpaduan kata listrik dan dinamis. Listris adalah listrik, sedangkan dinamis yaitu berubah-ubah atau bergerak.…
Gaya Gesek Untuk yang belum mengetahui apa itu gaya gesek disini akan mengulas tentang pengertian gaya gesek, rumus gaya gesek, dan contoh soalnya secara lengkap sebagai bahan refrensi anda. Oleh karena itu…
Pengertian Gerak Vertikal Ke Atas, Ciri, Rumus dan… Pengertian Gerak Vertikal Ke Atas, Ciri, Rumus dan Contoh Soal Gerak Vertikal Ke Atas Beserta Pembahasannya Lengkap – Gerak Vertikal Ke Atas (GVA) adalah salah satu bentuk gerak lurus yang termasuk…
Pengertian, Bunyi, Fungsi, Rumus dan Contoh Soal… Pengertian, Bunyi, Fungsi, Rumus dan Contoh Soal Hukum Kepler 1, 2, 3 (Kepler I, I, III) Lengkap – Hukum Kepler atau Hukum Gerakan Planet Kepler ditemukan oleh seorang matematikawan yang juga…
5 Contoh Soal Kimia Dan Pembahasan Terlengkap… Telah kita pelajari tentang pengertan termokimia pada postingan sebelumnya. Bahwa Termokimia adalah cabang ilmu kimia yang mempelajari tentang perubahan kalor atau energi yang menyertai suatu reaksi kimia, baik yang diserap…
Pengertian, Rumus & Contoh Soal Barisan Dan Deret… Pengertian, Rumus & Contoh Soal Barisan Dan Deret Geometri Beserta Penjelasan Lengkap – Terdapat dua jenis Barisan dan Deret di dalam matematika yaitu Barisan dan Deret Aritmatika & Barisan dan…
Tips Mengkonversi Satuan Massa, Panjang, Luas dan Volume Pada postingan sebelumnya sudah membahas cara mengkonversi satuan massa, cara mengkonversi satuan panjang, cara mengkonversi satuan luas, dan cara mengkonversi satuan volume. Cara tersebut agak ribet karena harus mengafal empat cara sekaligus agar menguasai…
Proporsi Proporsi Perbandingan/rasio dan proporsi merupakan dasar utama untuk memahami berbagai konsep dalam matematika maupun sains. Proporsi mengatakan bahwa dua perbandingan (atau dua pecahan) adalah sama. Dengan kalimat lain dua buah perbandingan dikatakan…
Hukum Ohm Ada yang sudah mengenal atau pernah mendengar mengenai Hukum Ohm? Oke, mari simak penjelasan secara lengkapnya dibawah ini ya. Pengertian Hukum Ohm Hukum ohm ini diperkenalkan oleh seorang ilmuwan yang…
Pengertian, Hubungan Massa Dengan Dinamika Partikel… Pengertian Dinamika Partikel, Hubungan Massa Dengan Dinamika Partikel dan Jenis Gaya Dalam Dinamika Partikel Terlengkap – Dinamika partikel merupakan ilmu yang mempelajari tentang gaya-gaya yang megakibatkan suatu partikel yang pada…
Matriks – Operasi Matriks, Rumus, Contoh Soal… Matriks – Operasi Matriks, Rumus, Contoh Soal Matriks dan Jawabannya Lengkap – Dalam matematika, matriks adalah susunan bilangan, simbol, atau ekspresi, yang disusun dalam baris dan kolom sehingga membentuk suatu bangun…
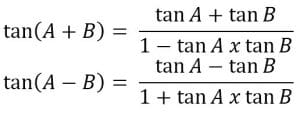
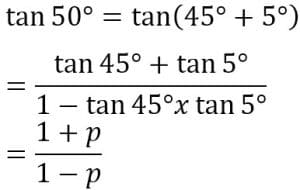
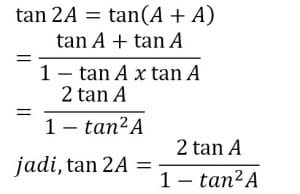
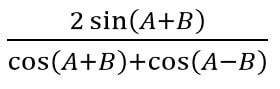
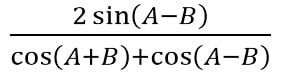