Pengertian Bangun Ruang : Macam Macam Bangun Ruang, Penjelasan dan Rumusnya Lengkap – Dalam matematika membahas tentang bangun ruang. Apa itu bangun ruang? Agar lebih memahaminya, kita akan membahas tentang pengertian bangun ruang, macam macam bangun ruang dan penjelasannya serta rumus bangun ruang secara lengkap.
Pengertian Bangun Ruang
Pengertian bangun ruang adalah sebuah penamaan atau sebutan untuk beberapa bangun-bangun yang berbentuk tiga dimensi atau bangun yang memiliki ruang yang dibatasi oleh sisi-sisinya.
Macam Macam Bangun Ruang dan Penjelasannya
Kubus
Pengertian kubus adalah bangun ruang tiga dimensi yang dibatasi oleh enam bidang kongruen berbentuk bujur sangkar atau persegi. Ciri-ciri kubus memiliki 6 sisi, 12 rusuk, dan 8 titik sudut.
Sifat-sifat kubus, diantaranya yaitu:
- Semua sisi kubus berbentuk persegi
- Semua rusuk kubus berukuran sama panjang
- Setiap diagonal bidang pada kubus memiliki ukuran yang sama panjang.
- Setiap diagonal ruang pada kubus memiliki ukuran yang sama panjang.
- Setiap bidang diagonal pada kubus memiliki bentuk persegi panjang.
Rumus Kubus
Rumus luas sisi kubus yaitu s²
Rumus luas permukaan kubus yaitu 6xs²
Rumus volume kubus yaitu sxsxs
Rumus keliling kubus yaitu 12xs
Keterangan:
L= Luas permukaan kubus (cm²)
V= Volume kubus (cm³)
S= Panjang rusuk kubus (cm)
Contoh Soal Bangun Ruang Kubus
1. Bak dalam kamar mandi Tria berbentuk kubus dengan kedalaman 1 meter. Bak tersebut diisi dengan air hingga penuh. Berapa liter air yang mengisi bak mandi Tria?
Cara Penyelesaian:
Diketahui : Kedalaman bak = rusuk kubus (s) : 1 meter
Ditanya : Volume (V)?
Jawab:
V: S3
V: s x s x s
V: 1 m x 1 m x 1 m
V: 1 m3
V: 1000 dm3
V: 1000 liter
Jadi air yang mengisi bak adalah 1000 liter.
Balok
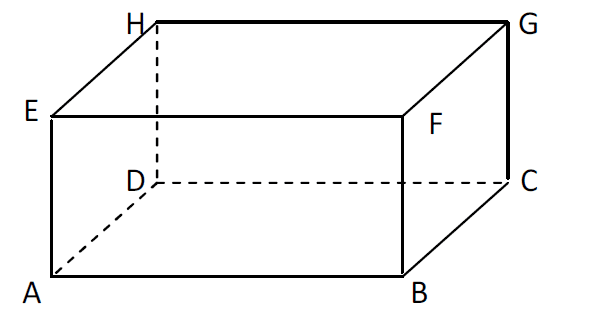
Pengertian balok adalah bangun ruang 3 dimensi yang dibentuk oleh tiga pasang persegi atau persegi panjang dengan paling tidak ada sepasang diantaranya berukuran berbeda. Balok memiliki 6 sisi, 12 rusuk dan 8 titik sudut. Balok memiliki sifat, unsur, dan juga rumus seperti luas permukaan, volume, bidang diagonal, diagonal bidang, dan diagonal ruang.
Sifat-sifat balok, diantaranya yaitu:
- Sisi-sisi balok berbentuk persegi panjang.
- Rusuk-rusuk yang sejajar memiliki ukuran sama panjang.
- Setiap diagonal bidang pada sisi yang berhadapan memiliki ukuran sama panjang.
- Setiap diagonal ruang pada balok memiliki ukuran sama panjang.
- Setiap bidang diagonal pada balok memiliki bentuk persegi panjang.
Rumus Balok
Rumus permukaan balok= 2x(pxl)+(pxt)+(lxt)
Rumus diagonal ruang = (p² + l² + t²)²
Rumus untuk keliling balok= 4x (p+l+t)
Rumus untuk volume balok= p x l x t
Keterangan:
P = Panjang (cm)
L = Lebar (cm)
T =Tinggi (cm)
Contoh Soal Bangun Ruang Balok
1. Sebuah balok memiliki panjang 12 cm, lebar 8 cm dan tinggi 4 cm. Hitunglah berapa panjang diagonal ruang balok?
Cara Penyelesaian:
Diketahui:
p = 12 cm
l = 8 cm
t = 4 cm
Ditanya: Diagonal ruang (Dr)?
Jawab:
Dr : √(p²+l²+t²)
Dr : √(12²+8²+4²)
Dr : √244
Dr : 4√14
Limas
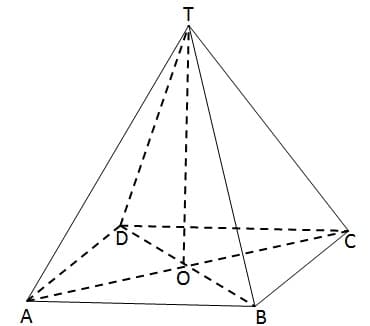
Pengertian limas adalah bangun ruang 3 dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga dengan titik puncak yang saling berhimpit. Limas memiliki n+1 sisi, 2n rusuk dan n+1 titik sudut.
Sifat- sifat limas, diantaranya yaitu
- Memiliki 5 sisi yaitu: 1 sisi berbentuk segiempat yang merupakan alas dan 4 sisi lainnya semuanya berbentuk segitiga serta merupakan sisi tegak.
- Memiliki 8 buah rusuk
- Memiliki 5 titik sudut yaitu: 4 sudut berada di bagian alas dan 1 sudut berada di bagian atas yang merupakan titik puncak.
Rumus Limas
Luas Permukaan Limas
L = Luas alas + Luas Selumbung Limas
L = Luas alas + 1/4 x keliling alas x tinggi segitiga
Volume Limas
V= 1/3.Luas alas.tinggi
Contoh Soal Bangun Ruang Limas
Sebuah limas memiliki alas berbentuk persegi dengan sisi 12 cm. Tentukan volume limas jika tingginya 30 cm!
Cara Penyelesaian:
Diketahui :
sisi alas = 12 cm
tinggi limas = 30 cm
Ditanya : volume limas?
Jawab :
V = 1/3.Luas alas.tinggi
V = 1/3.(sxs).t
V = 1/3.(12×12).30
V = 1440 cm³
Bola
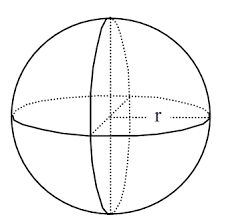
Pengertian bola adalah bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang disebut dengan titik pusat bola dan bola hanya memiliki 1 sisi.
Sifat-sifat bola, diantaranya yaitu:
- Memiliki 1 buah sisi.
- Memiliki 1 buah titik pusat.
- Tidak memiliki titik sudut.
- Memiliki jari jari yang tak terhingga dan semuanya sama panjang.
Rumus Bola
Rumus volume bola : 4/3 x π x r³
Rumus luas bola : 4 x π x r²
Keterangan:
V : Volume bola (cm³)
L : Luas permukaan bola (cm²)
R : Jari-jari bola (cm)
π : 22/7 atau 3,14
Contoh Soal Bangun Ruang Bola
Sebuah bola berdiameter 24 cm. Berapakah volume bola tersebut?
Cara Penyelesaian:
Diketahui :
d = 24 cm
r = 1/2. d
r = 1/2. 24
r = 12 cm
Ditanya : Volume bola?
Jawab :
v = 4/3 π x r³
V = 4/3 x 22/7 x 12³
V = 4/3 x 22/7 x 1728
V = 7234,56 cm³
Kerucut
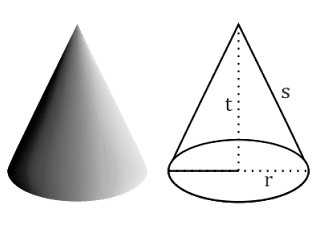
Pengertian kerucut adalah salah satu bangun ruang yang mempunyai sebuah alas yang berbentuk lingkaran dengan selimut yang memiliki irisan dari lingkaran.
Sifat-sifat kerucut, diantaranya:
- Memiliki 2 sisi (1 sisi merupakan alas yang berbentuk lingkaran dan 1 sisinya lagi berupa sisi lengkung atau selimut kerucut)
- Memiliki 1 rusuk
- Memiliki 1 titik sudut
Rumus Kerucut
Rumus volume kerucut = 1/3 x π x r x r x t
Rumus luas kerucut = luas alas+luas selimut
Keterangan:
r = jari-jari (cm)
T = tinggi(cm)
π = 22/7 atau 3,14
Contoh Soal Bangun Ruang Kerucut
1. Sebuah lingkaran memiliki luas 40 cm². Jika lingkaran tersebut dibuat menjadi kerucut dengan tinggi 9 cm, hitung volume kerucut tersebut.
Jawaban:
Diketahui:
t = 9 cm
Luas : L = π x r² = 40 cm² .
V = 1/3 x π x r² x t
= 1/3 x 40 x 9 (ingat : π x r² = 40 cm²)
= 120 cm³.
Jadi Volume kerucut adalah 120 cm³.
Tabung
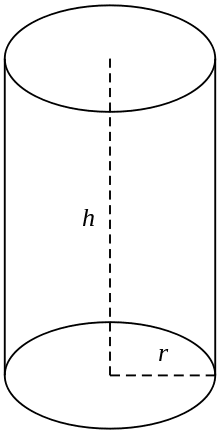
Pengertian tabung adalah sebuah bangun ruang tiga dimensi yang memiliki tutup dan alas yang berbentuk sebuah lingkaran dengan ukuran yang sama dengan di selimuti oleh persegi panjang. Tabung juga disebut dengan silinder.
Sifat-sifat tabung, diantaranya yaitu:
- Memiliki 2 (dua) buah rusuk lengkung.
- Memiliki alas dan tutup berbentuk lingkaran yang masing-masing sama besar.
- Memiliki 3 (tiga) buah sisi diantaranya dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang.
- Tidak memiliki titik sudut
Rumus Tabung
Rumus keliling alas tabung = 2πr
Rumus volume tabung (V) = πr²t
Rumus luas permukaan tabung (L) = 2πr²
Rumus luas tutup tabung : 2πr
Rumus luas alas tabung : 2πr
Rumus luas selimut tabung : 2πr²t
Rumus luas tabung tanpa tutup = π x r2 + 2 x π x r x t = π x r (r + 2t)
Rumus luas jaring-jaring tabung = alas x tinggi = a x t
Rumus volume gabungan tabung dan kerucut yaitu ( π.r².t )+( 1/3.π.r².t )
Rumus luas gabungan tabung dan kerucut yaitu (π.r²)+(2.π.r.t)+(π.r.s)
Rumus volume gabungan tabung dan setengah bola yaitu π.r².t+2/3. π.r3
Rumus luas gabungan tabung dan setengah bola (π.r²)+(2.π.r.t)+(½.4.n.r²) = (3.π.r²)+(2. π .r.t)
Rumus volume gabungan tabung dan bola yaitu (π.r².t)+(4/3. π.r3)
Rumus luas gabungan tabung dan bola yaitu (2. π.r²)+(4. π.r²) = π.r²
Keterangan:
V = Volume tabung(cm³)
π = 22/7 atau 3,14
r = Jari – jari /setengah diameter (cm)
t = Tinggi (cm)
Contoh Soal Bangun Ruang Tabung
1. Berapakah volume sebuah tabung yang memiliki sebuah diameter 60 cm dan tinggi 70 cm?
Jawab :
diameter = 60 cm, karena r = 1/2 diameter maka r = 30 cm
tinggi = 70 cm
Volume Tabung = π x r² x t
= (22/7) x 30² x 70
= (22/7) x 30 x 30 x 70
= (22/7) x 63000
= 198.000 cm³.
Prisma
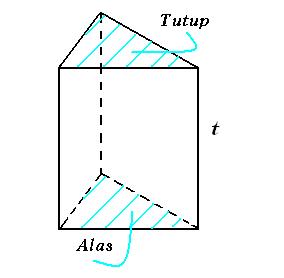
Pengertian prisma adalah salah satu bentuk bangun ruang yang dibatasi oleh 2 bangun datar yang kongruen (sama dan sebangun) dan sejajar. Dua bangun yang membatasi tersebut disebut dengan bidang alas dan bidang atas/tutup.
Sifat-sifat prisma, diantaranya:
Prisma memiliki bentuk alas dan atap yang kongruen (sama dan sebangun).
Setiap sisi bagian samping prisma berbentuk persegi panjang.
Prisma memiliki rusuk yang tegak dan adapula yang tidak tegak.
Setiap diagonal bidang bidang pada sisi yang sama memiliki ukuran yang sama.
Rumus Prisma
Luas Permukaan Prisma
L = 2 Luas alas + (Keliling alas x tinggi)
Volume Prisma
V = Luas alas x Tinggi
Contoh Soal Bangun Ruang Prisma
1. Volume Prisma yang memiliki luas alas 38 cm² dan panjang 45 cm adalah…..
Cara Penyelesaian:
Diketahui:
Luas alas : 38 cm²
Tinggi : 45 cm
Ditanya : Volume (v) ?
Jawab
V = Luas alas x tinggi
V = 38 x 45
V = 1710 cm³
Jadi volume prisma tersebut adalah 1710 cm³
Demikian materi tentang bangun ruang, jenis dan rumus bangun ruang lengkap, semoga bermanfaat dan jangan lupa ikuti postingan lainnya.