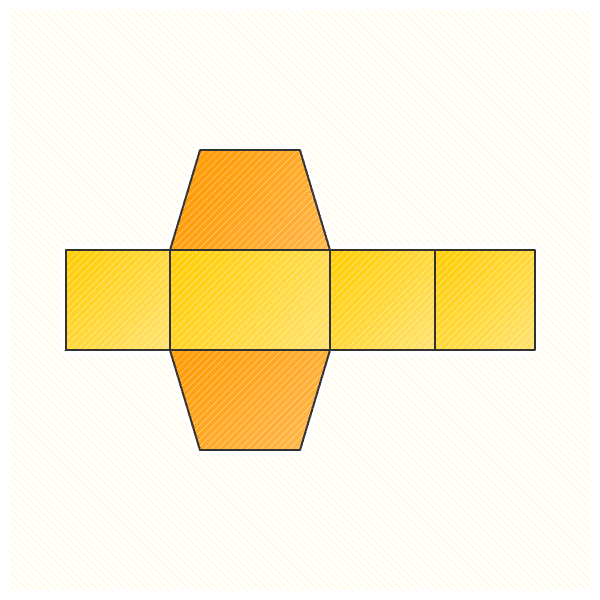Prisma – Sifat, Unsur, Jaring-Jaring Prisma, Rumus (Luas Permukaan Prisma dan Volume Prisma) dan Contoh Soal Lengkap – Prisma adalah salah satu bentuk bangun ruang yang dibatasi oleh 2 bangun datar yang kongruen (sama dan sebangun) dan sejajar. Dua bangun yang membatasi tersebut disebut dengan bidang alas dan bidang atas/tutup.
Ada banyak macam jenis Prisma diantaranya Prisma segitiga, Prisma segilima, Prisma segi enam, Prisma trapesium, Prisma belah ketupat dan lain sebagainya. Berikut adalah contoh dari bangun Prisma :
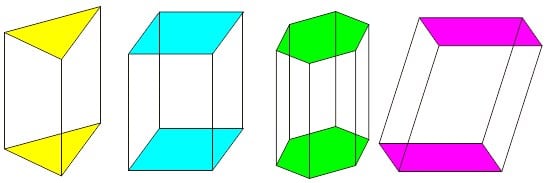
Kali ini kita akan membahas tentang Sifat-Sifat Prisma, Unsur-Unsur Prisma, serta Jaring-Jaring Prisma dan juga rumus untuk mengetahui luas permukaan dan volume prisma, berikut selngkapnya:
Sifat-Sifat Prisma
- Prisma memiliki bentuk alas dan atap yang kongruen (sama dan sebangun).
- Setiap sisi bagian samping prisma berbentuk persegi panjang.
- Prisma memiliki rusuk yang tegak dan adapula yang tidak tegak.
- Setiap diagonal bidang bidang pada sisi yang sama memiliki ukuran yang sama.
Unsur-Unsur Prisma
Berikut adalah unsur-unsur dari Prisma segi enam:
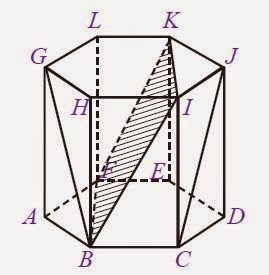
Sisi atau Bidang
Prisma segi enam memiliki 8 sisi atau bidang. Perhatikan gambar diatas yang merupakan sisi atau bidang prisma segienam, adalah:
Sisi alas = ABCDEF
Sisi atas = GHIJK
Sisi depan = BCIH
Sisi belakang = FEKL
Sisi Depan Kanan = ABHG
Sisi Belakang Kanan = AFLG
Sisi Depan Kiri = CDJI
Sisi Belakang Kiri = DEKJ
Rusuk
Prisma segi enam memiliki 18 rusuk, 6 diantaranya rusuk tegak. Perhatikan gambar diatas, yang merupakan rusuk yaitu AB, BC, CD, DE, EF, FA, GH, HI, IJ, JK, KL,LG, rusuk tegaknya yaitu AG, BH, CI, DJ, EK, FL.
Titik Sudut
Prisma segi enam memiliki 12 titik sudut yaitu A,B,C,D,E,F,G,H,I,J,K,dan L.
Diagonal Bidang
Prisma segienam memiliki 16 Diagonal Bidang atau Diagonal sisi, perhatikan gambar diatas yang merupakan diagonal bidang diantaranya : BG,CJ,BI,AH,HC,ID,DK,JE,KF,LE,LA,GF,HK,IL,BE,dan CF.
Bidang Diagonal
Perhatikan gambar diatas yang merupakan bidang diagonal diantaranya BFKI, ECHL, KLBC,HIEF dan lain sebagainya.
Diagonal Ruang
Perhatikan gambar Prisma segienam diatas terdapat 36 diagonal ruang, yang merupakan diagonal ruang antara lain AI,AJ,AK,BJ,BK,BL dan lain sebagainya.
Jaring-Jaring Prisma
Jaring-Jaring Prisma Segitiga
Jaring-Jaring Prisma Segi Lima
1.
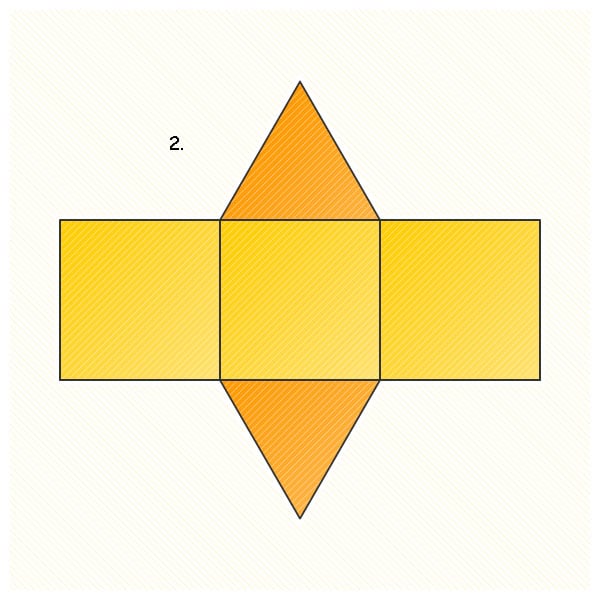
2.
3.

Jaring-Jaring Prisma Segi Enam
1.
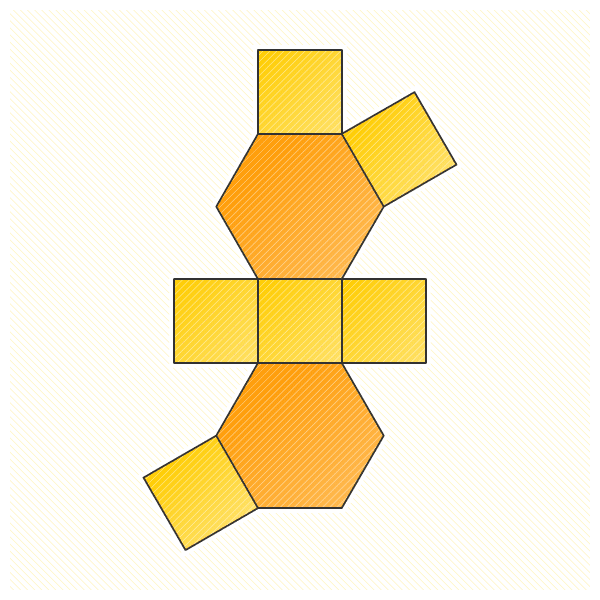
2.
Jaring-Jaring Prisma Trapesium Sama Kaki
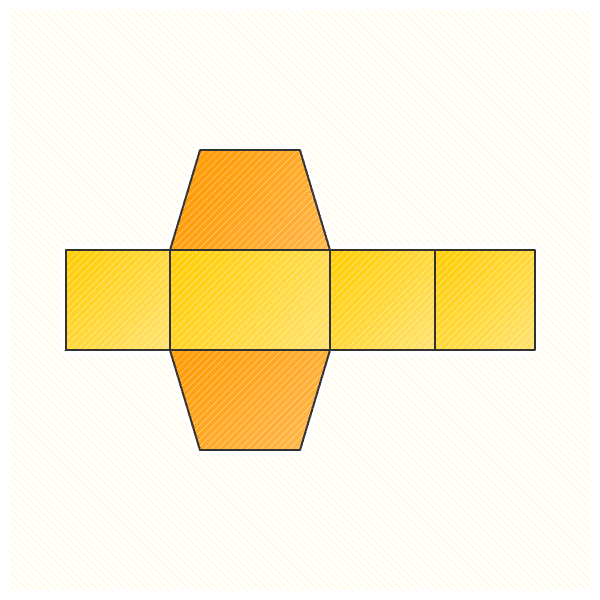
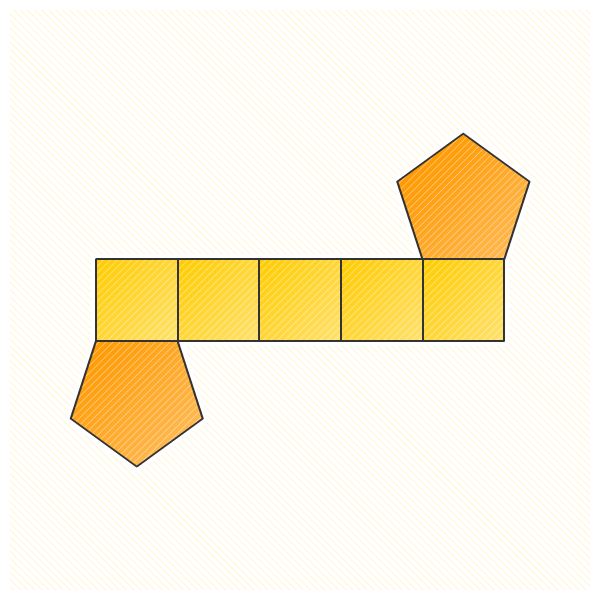
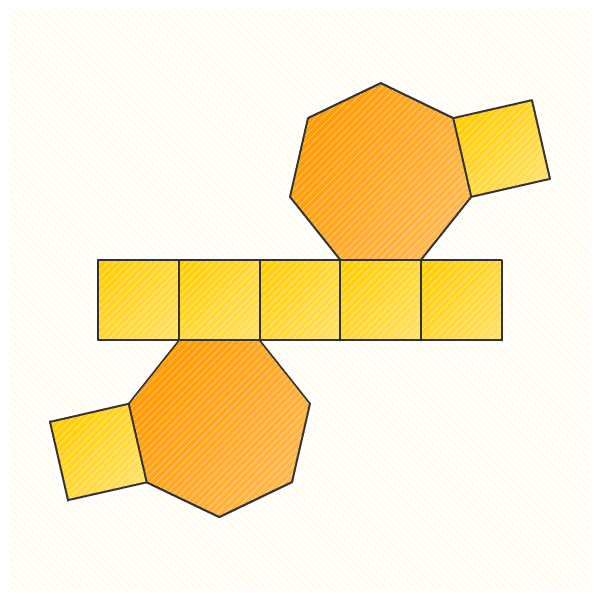
Jaring-Jaring Prisma Segi Tujuh
Rumus Bangun Ruang Prisma
Luas Permukaan Prisma
L = 2 Luas alas + (Keliling alas x tinggi)
Volume Prisma
V = Luas alas x Tinggi
Contoh Soal
1. Volume Prisma yang memiliki luas alas 38 cm2 dan panjang 45 cm adalah…..
Cara Penyelesaian:
Diketahui:
Luas alas : 38 cm2
Tinggi : 45 cm
Ditanya : Volume (v) ?
Jawab
V = Luas alas x tinggi
V = 38 x 45
V = 1710 cm3Jadi volume prisma tersebut adalah 1710 cm3
2. Volume sebuah prisma segitiga adalah 186 cm3. Luas alas prisma tersebut adalah 31 cm2. tinggi prisma tersebut adalah……
Cara Penyelesaian:
Diketahui:
Volume = 186 cm3
Tinggi = 31 cm2
Ditanya: Tinggi (t) ?
Jawab :
V = Luas alas x tinggi
186 = 31 x t
31 x t = 186
t = 186/31
t = 6 cmJadi tinggi prisma tersebut adalah 6 cm.
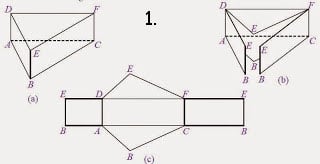
3.Perhatikan gambar dibawah ini!
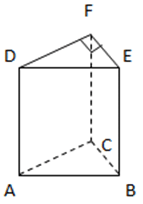
Diketahui panjang AC = 12 cm, BC = 9 cm dan BE = 46 cm, maka berapakah besar volume prisma tersebut!
Cara Penyelesaian:
Diketahui :
BC = Alas = 9 cm
AC = Tinggi alas = 12 cm
Be = Tinggi = 46 cm
Ditanya: Volume (V)?
Jawab :
Luas alas = 1/2 x alas x tinggi
Luas alas = 1/2 x 9 x 12
Luas alas = 54 cm2Volume = luas alas x tinggi
Volume = luas alas x BE
Volume = 54 x 46
Volume = 2.484 cm3
Jadi volume prisma tersebut adalah 2.484 cm3.
4. Perhatikan gambar prisma dibawah ini!
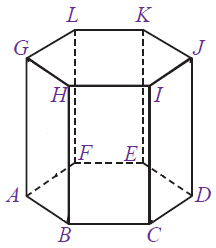
Jika diketahui IJ = 6 cm dan AG = 10√3 cm, tentukan luas permukaan prisma segi enam beraturan diatas!
Cara Penyelesaian:
Diketahui :
IJ = 6 cm
AG = 10√3 cm
Ditanya : Luas Permukaan (L) ?
Jawab :
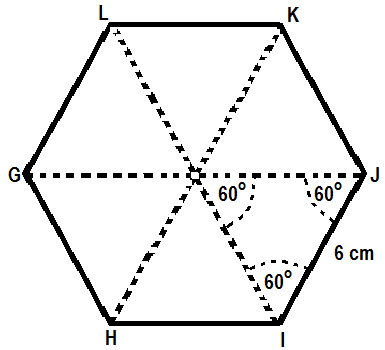
cari luas segitiga sama sisi tersebut, caranya :
L∆ = ¼r2√3
L∆ = ¼ (6 cm)2√3
L∆ = 9√3 cm2
Luas alas prisma:
L = 6 x L∆
L = 6 x 9√3 cm2
L = 54√3 cm2
Luas sisi tegak yaitu Keliling alas dikali tinggi prisma:
L = 6r x t
L = 6.6 cm x 10√3
L = 360√3 cm2
Luas Permukaan Prisma
L = 2 x luas alas = luas sisi tegak
L = 2 x 54√3 cm2+ 360√3 cm2
L = 468√3 cm2
5. Alas sebuah prisma berbentuk belah ketupat dengan panjang diagonal masing-masing 12 cm dan 16 cm. Jika tinggi prisma 18 cm, hitunglah panjang sisi belah ketupat, luas alas prisma dan luas permukaan prisma!
Cara Penyelesaian:
Cari panjang sisi belah ketupat teorema Phytagoras, yakni:s = √(6
2 + 8
2)
s = √(36 + 64)
s = √100
s = 10 cm
K alas = 4.s
K alas = 4.10 cm
K alas = 40 cm
L alas = ½ x d1 x d2
L alas = ½ x 12 cm x 16 cm
L alas = 96 cm2
L = 2 x L alas + K alas . t
L = 2 x 96 cm2 + 40 cm . 18 cm
L = 192 cm2+ 720 cm2
L = 912 cm2
6. Sebuah prisma alasnya berbentuk persegi panjang dengan luas alas 24 cm2. Jika lebar persegi panjang 4 cm dan tinggi prisma 10 cm, hitunglah luas permukaan prisma.
Cara Penyelesaian:
Cari panjang persegi panjang, yakni:
L = p . l
24 cm2 = p . 4 cm
p = 6 cmK alas = 2(p + l)
K alas = 2(6 cm + 4 cm)
K alas = 20 cm
L = 2 x L alas + K alas . t
L = 2 x 24 cm2 + 20 cm . 10 cm
L = 48 cm2 + 200 cm2
L = 248 cm2
Demikian penjelasan yang bisa kami sampaikan tentang Prisma – Sifat, Unsur, Jaring-Jaring Prisma, Rumus Prisma dan Contoh Soal Lengkap . Semoga bermanfaat dan sampai jumpa pada postingan selanjutnya.
Artikel Paling Populer :
- Molaritas, Molalitas, Normalitas, Fraksi Mol Ada yang sudah mengenal atau pernah mendengar mengenai Molaritas, Molalitas, Normalitas, dan Fraksi Mol? 1. Mol Larutan (n) Mol merupakan massa (gram) pada suatu zat dibagi dengan massa molekul relatif atau berat…
- Ciri-Ciri, Klasifikasi Dan Pengelompokkan Mollusca Masih ingat dengan postingan mengenai Invertebrata , disitu disebutkan bahwa Hewan-hewan yang termasuk kelompok Invertebrata, antara lain Porifera (hewan berpori), Cnidaria (hewan bersengat), Platyhelminthes (cacing pipih), Nemathelminthes (cacing benang/ cacing gilik), Annelida (cacing…
- Bangun Datar – Pengertian, Macam-Macam, Sifat-Sifat,… Bangun Datar – Pengertian, Macam-Macam Jenis Bangun Datar, Sifat-Sifat Bangun Datar, dan Rumus Bangun Datar Serta Contoh Soal Bangun Datar Terlengkap – Bangun datar adalah sebutan untuk bangun-bangun dua dimensi, gabungan bangun datar…
- Pengertian, Rumus dan Contoh Soal Molaritas,… Pengertian, Rumus dan Contoh Soal Molaritas, Pembuatan Larutan dan Pengenceran Lengkap – Kali ini kita aka membahas tentang pengertian dan rumus molaritas, pembuatan larutan dan pengenceran beserta dengan contoh soal dan…
- Bidang Miring Pesawat sederhana digunakan untuk memudahkan pelaksanaan pekerjaan, walaupun membutuhkan waktu yang lebih lama (lintasan lebih jauh). Pada kesempatan kali ini kita akan membahas mengenai bidang miring. Untuk lebih jelasnya bacalah…
- Rumus Layang-Layang : Pengertian, Sifat, Menghitung… Rumus Luas dan Keliling Layang-Layang – Bangun layang-layang adalah? Apa rumus layang-layang? Sebutkan sifat-sifat layang-layang! Agar lebih memahaminya, kali ini kita akan membahas tentang pengertian bangun layang-layang, sifat, gambar, rumus, contoh…
- Pengertian, Sifat, Rumus, dan Contoh Soal… Pengertian, Sifat, Rumus, Jawaban dan Contoh Soal Layang-Layang Beserta Pembahasan Lengkap – Layang-layang adalah bangun datar 2 dimensi yang dibentuk oleh 2 pasang rusuk yang masing-masing pasangan sama panjang dan…
- Bola – Ciri, Contoh Soal Beserta Penyelesaian Luas… Bola – Ciri, Contoh Soal Beserta Penyelesaian Luas Permukaan dan Volume Bola Lengkap – Bola merupakan bangun ruang tiga dimensi yang dibentuk oleh titik-titik yang berjarak sama terhadap suatu titik yang…
- Pengertian, Rumus dan Contoh Soal Perpindahan Kalor… Pengertian, Rumus dan Contoh Soal Perpindahan Kalor Secara Radiasi (Pancaran) Beserta Pemahaman Terlengkap – Jarak dari bumi ke matahari mencapai 149.600.000 km dan antara bumi dan matahari terdapat ruang hampa udara,…
- Alat Optik Ada yang sudah mengenal atau pernah mendengar mengenai Alat Optik? Oke, mari simak penjelasan secara lengkapnya dibawah ini ya. Pengertian Alat Optik Alat Optik ialah suatu alat penglihatan manusia, baik alamiah…
- Hujan Salju Ada yang sudah mengenal atau pernah mendengar mengenai istilah Hujan Salju? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Hujan Salju Kata Salju berasal dari bahasa arab yaitu “Tsalju” yang artinya…
- Jaringan Meristem Ada yang sudah mengenal atau pernah mendengar mengenai istilah Jaringan Meristem? Simak penjelasan terlengkapnnya di bawah ini. Pengertian Jaringan Meristem Jaringan meristem merupakan salah satu jaringan yang sel – selnya…
- Pengertian, Bunyi, Rumus, Penerapan dan Contoh Soal… Pengertian, Bunyi, Rumus, Penerapan dan Contoh Soal Hukum Boyle Terlengkap – Hukum Boyle adalah hukum fisika yang menjelaskan tentang bagaimana kaitan antara tekanan dengan volume suatu gas. Penemu hukum boyle ini adalah Robert Boyle…
- Pembahasan Lengkap Aturan Cosinus Segitiga… Pembahasan Lengkap Aturan Cosinus Segitiga Trigonometri Dalam Ilmu Matematika – Teorema Pythagoras merupakan suatu rumus matematika yang sangat penting dalam geometri. Dengan menggunakan teorema phytagoras, kita bisa menghitung jarak antara dua…
- Pengertian dan Jenis-Jenis Segitiga Mungkin Anda tidak asing dengan yang namanya segitiga. Contoh penerapan segitiga yang sering Anda jumpai adalah penggaris yang berbentuk segitiga. Apa sih sebenarnya segitiga itu? dan ada berapa jenis-jenis segitiga?…
- Pengertian gaya Gesek dengan Rumus dan Contoh Soal… Pengertian Gaya Gesek Lengkap dengan Rumus dan Pembahasan Contoh Soal Gaya gesek merupakan gaya yang melawan gerak benda pada suatu permukaan yang terjadi akibat oleh dua permukaan benda yang bersentuhan.…
- Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan… Pengertian Senyawa Kimia, Ciri, Sifat, Jenis dan Tata Nama Senyawa Kimia Beserta Contohnya Lengkap – Senyawa kimia adalah zat kimia murni yang terdiri dari dua atau beberapa unsur yang bisa…
- Gaya Gesek Untuk yang belum mengetahui apa itu gaya gesek disini akan mengulas tentang pengertian gaya gesek, rumus gaya gesek, dan contoh soalnya secara lengkap sebagai bahan refrensi anda. Oleh karena itu…
- Sifat-Sifat Penjumlahan dan Pengurangan Pecahan Sifat-sifat penjumlahan dan pengurangan pecahan sama seperti sifat-sifat penjumlahan bulangan bulat. Pada bilangan bulat kita mengenal lima sifat yakni sifat tertutup, sifat komutatif, sifat asosiatif, mempunyai unsur identitas, dan mempunyai invers. Kelima…
- Cermin Cembung : Pengertian, Sinar Istimewa, Sifat… Cermin Cembung: Pengertian, Sinar Istimewa, Sifat Bayangan, Rumus dan Contoh Soal Cermin Cembung Terlengkap – Cermin Cembung adalah cermin yang memiliki bentuk lengkung, dimana permukaan cermin yang memantulkan cahaya melengkungke…